$\require{mathtools}
%
%%% GENERIC MATH %%%
%
% Environments
\newcommand{\al}[1]{\begin{align}#1\end{align}} % need this for \tag{} to work
\renewcommand{\r}{\mathrm}
%
% Greek
\newcommand{\eps}{\epsilon}
\newcommand{\veps}{\varepsilon}
\let\fi\phi % because it looks like an f
\let\phi\varphi % because it looks like a p
%
% Miscellaneous shortcuts
% .. over and under
\newcommand{\ss}[1]{_{\substack{#1}}}
\newcommand{\ob}{\overbrace}
\newcommand{\ub}{\underbrace}
\newcommand{\ol}{\overline}
\newcommand{\tld}{\widetilde}
\newcommand{\HAT}{\widehat}
\newcommand{\f}{\frac}
\newcommand{\s}[2]{#1 /\mathopen{}#2}
\newcommand{\rt}{\sqrt}
% .. relations
\newcommand{\sr}{\stackrel}
\newcommand{\sse}{\subseteq}
\newcommand{\ce}{\coloneqq}
\newcommand{\ec}{\eqqcolon}
\newcommand{\ap}{\approx}
\newcommand{\ls}{\lesssim}
\newcommand{\gs}{\greatersim}
% .. miscer
\newcommand{\q}{\quad}
\newcommand{\qq}{\qquad}
\newcommand{\heart}{\heartsuit}
%
% Delimiters
% (I needed to create my own because the MathJax version of \DeclarePairedDelimiter doesn't have \mathopen{} and that messes up the spacing)
% .. one-part
\newcommand{\p}[1]{\mathopen{}\left( #1 \right)}
\newcommand{\b}[1]{\mathopen{}\left[ #1 \right]}
\newcommand{\set}[1]{\mathopen{}\left\{ #1 \right\}}
\newcommand{\abs}[1]{\mathopen{}\left\lvert #1 \right\rvert}
\newcommand{\floor}[1]{\mathopen{}\left\lfloor #1 \right\rfloor}
\newcommand{\ceil}[1]{\mathopen{}\left\lceil #1 \right\rceil}
\newcommand{\inner}[1]{\mathopen{}\left\langle #1 \right\rangle}
% .... (use phantom to force at least the standard height of double bars)
\newcommand{\norm}[1]{\mathopen{}\left\lVert #1 \vphantom{f} \right\rVert}
\newcommand{\frob}[1]{\norm{#1}_\mathrm{F}}
%% .. two-part
\newcommand{\incond}[2]{#1 \mathop{}\middle|\mathop{} #2}
\newcommand{\cond}[2]{ {\left.\incond{#1}{#2}\right.}}
\newcommand{\pco}[2]{\p{\incond{#1}{#2}}}
\newcommand{\bco}[2]{\b{\incond{#1}{#2}}}
\newcommand{\setco}[2]{\set{\incond{#1}{#2}}}
\newcommand{\at}[2]{\left.#1\right|_{#2}}
% ..... (use phantom to force at least the standard height of double bar)
\newcommand{\oldpara}[2]{#1\vphantom{f} \mathop{}\middle\|\mathop{} #2}
%\newcommand{\para}[2]{#1\vphantom{f} \mathop{}\middle\|\mathop{} #2}
\newcommand{\para}[2]{\mathchoice{\begin{matrix}#1\\\hdashline#2\end{matrix}}{\begin{smallmatrix}#1\\\hdashline#2\end{smallmatrix}}{\begin{smallmatrix}#1\\\hdashline#2\end{smallmatrix}}{\begin{smallmatrix}#1\\\hdashline#2\end{smallmatrix}}}
\newcommand{\ppa}[2]{\p{\para{#1}{#2}}}
\newcommand{\bpa}[2]{\b{\para{#1}{#2}}}
%\newcommand{\bpaco}[4]{\bpa{\incond{#1}{#2}}{\incond{#3}{#4}}}
\newcommand{\bpaco}[4]{\bpa{\cond{#1}{#2}}{\cond{#3}{#4}}}
%
% Levels of closeness
\newcommand{\scirc}[1]{\sr{\circ}{#1}}
\newcommand{\sdot}[1]{\sr{.}{#1}}
\newcommand{\slog}[1]{\sr{\log}{#1}}
\newcommand{\createClosenessLevels}[7]{
\newcommand{#2}{\mathrel{(#1)}}
\newcommand{#3}{\mathrel{#1}}
\newcommand{#4}{\mathrel{#1\!\!#1}}
\newcommand{#5}{\mathrel{#1\!\!#1\!\!#1}}
\newcommand{#6}{\mathrel{(\sdot{#1})}}
\newcommand{#7}{\mathrel{(\slog{#1})}}
}
\let\lt\undefined
\let\gt\undefined
% .. vanilla versions (is it within a constant?)
\newcommand{\ez}{\scirc=}
\newcommand{\eq}{\simeq}
\newcommand{\eqq}{\mathrel{\eq\!\!\eq}}
\newcommand{\eqqq}{\mathrel{\eq\!\!\eq\!\!\eq}}
\newcommand{\lez}{\scirc\le}
\newcommand{\lq}{\preceq}
\newcommand{\lqq}{\mathrel{\lq\!\!\lq}}
\newcommand{\lqqq}{\mathrel{\lq\!\!\lq\!\!\lq}}
\newcommand{\gez}{\scirc\ge}
\newcommand{\gq}{\succeq}
\newcommand{\gqq}{\mathrel{\gq\!\!\gq}}
\newcommand{\gqqq}{\mathrel{\gq\!\!\gq\!\!\gq}}
\newcommand{\lz}{\scirc<}
\newcommand{\lt}{\prec}
\newcommand{\ltt}{\mathrel{\lt\!\!\lt}}
\newcommand{\lttt}{\mathrel{\lt\!\!\lt\!\!\lt}}
\newcommand{\gz}{\scirc>}
\newcommand{\gt}{\succ}
\newcommand{\gtt}{\mathrel{\gt\!\!\gt}}
\newcommand{\gttt}{\mathrel{\gt\!\!\gt\!\!\gt}}
% .. dotted versions (is it equal in the limit?)
\newcommand{\ed}{\sdot=}
\newcommand{\eqd}{\sdot\eq}
\newcommand{\eqqd}{\sdot\eqq}
\newcommand{\eqqqd}{\sdot\eqqq}
\newcommand{\led}{\sdot\le}
\newcommand{\lqd}{\sdot\lq}
\newcommand{\lqqd}{\sdot\lqq}
\newcommand{\lqqqd}{\sdot\lqqq}
\newcommand{\ged}{\sdot\ge}
\newcommand{\gqd}{\sdot\gq}
\newcommand{\gqqd}{\sdot\gqq}
\newcommand{\gqqqd}{\sdot\gqqq}
\newcommand{\ld}{\sdot<}
\newcommand{\ltd}{\sdot\lt}
\newcommand{\lttd}{\sdot\ltt}
\newcommand{\ltttd}{\sdot\lttt}
\newcommand{\gd}{\sdot>}
\newcommand{\gtd}{\sdot\gt}
\newcommand{\gttd}{\sdot\gtt}
\newcommand{\gtttd}{\sdot\gttt}
% .. log versions (is it equal up to log?)
\newcommand{\elog}{\slog=}
\newcommand{\eqlog}{\slog\eq}
\newcommand{\eqqlog}{\slog\eqq}
\newcommand{\eqqqlog}{\slog\eqqq}
\newcommand{\lelog}{\slog\le}
\newcommand{\lqlog}{\slog\lq}
\newcommand{\lqqlog}{\slog\lqq}
\newcommand{\lqqqlog}{\slog\lqqq}
\newcommand{\gelog}{\slog\ge}
\newcommand{\gqlog}{\slog\gq}
\newcommand{\gqqlog}{\slog\gqq}
\newcommand{\gqqqlog}{\slog\gqqq}
\newcommand{\llog}{\slog<}
\newcommand{\ltlog}{\slog\lt}
\newcommand{\lttlog}{\slog\ltt}
\newcommand{\ltttlog}{\slog\lttt}
\newcommand{\glog}{\slog>}
\newcommand{\gtlog}{\slog\gt}
\newcommand{\gttlog}{\slog\gtt}
\newcommand{\gtttlog}{\slog\gttt}
%
% Miscellaneous
\newcommand{\LHS}{\mathrm{LHS}}
\newcommand{\RHS}{\mathrm{RHS}}
% .. operators
\DeclareMathOperator{\poly}{poly}
\DeclareMathOperator{\polylog}{polylog}
\DeclareMathOperator{\quasipoly}{quasipoly}
\DeclareMathOperator{\negl}{negl}
\DeclareMathOperator*{\argmin}{arg\,min}
\DeclareMathOperator*{\argmax}{arg\,max}
% .. functions
\DeclareMathOperator{\id}{id}
\DeclareMathOperator{\sign}{sign}
\DeclareMathOperator{\err}{err}
\DeclareMathOperator{\ReLU}{ReLU}
% .. analysis
\let\d\undefined
\newcommand{\d}{\operatorname{d}\mathopen{}}
\newcommand{\df}[2]{\f{\d #1}{\d #2}}
\newcommand{\ds}[2]{\s{\d #1}{\d #2}}
\newcommand{\part}{\partial}
\newcommand{\partf}[2]{\f{\part #1}{\part #2}}
\newcommand{\parts}[2]{\s{\part #1}{\part #2}}
\newcommand{\grad}[1]{\mathop{\nabla\!_{#1}}}
% .. sets
\newcommand{\N}{\mathbb{N}}
\newcommand{\Z}{\mathbb{Z}}
\newcommand{\R}{\mathbb{R}}
\newcommand{\C}{\mathbb{C}}
\newcommand{\F}{\mathbb{F}}
\newcommand{\zo}{\set{0,1}}
\newcommand{\pmo}{\set{\pm 1}}
%
%%% SPECIALIZED MATH %%%
%
% Logic
\renewcommand{\and}{\wedge}
\newcommand{\AND}{\bigwedge}
\newcommand{\or}{\vee}
\newcommand{\OR}{\bigvee}
\newcommand{\xor}{\oplus}
\newcommand{\XOR}{\bigoplus}
\newcommand{\union}{\cup}
\newcommand{\inter}{\cap}
\newcommand{\UNION}{\bigcup}
\newcommand{\INTER}{\bigcap}
\newcommand{\comp}{\overline}
\newcommand{\true}{\r{true}}
\newcommand{\false}{\r{false}}
\newcommand{\tf}{\set{\true,\false}}
\DeclareMathOperator{\One}{\mathbb{1}}
\DeclareMathOperator{\1}{\mathbb{1}}
%
% Linear algebra
\renewcommand{\span}{\mathrm{span}}
\DeclareMathOperator{\rank}{rank}
\DeclareMathOperator{\proj}{proj}
\DeclareMathOperator{\dom}{dom}
\DeclareMathOperator{\Img}{Im}
\newcommand{\transp}{\mathsf{T}}
\renewcommand{\t}{^\transp}
% ... named tensors
\newcommand{\namedtensorstrut}{\vphantom{fg}} % milder than \mathstrut
\newcommand{\name}[1]{\mathsf{\namedtensorstrut #1}}
\newcommand{\nbin}[2]{\mathbin{\underset{\substack{#1}}{\namedtensorstrut #2}}}
\newcommand{\ndot}[1]{\nbin{#1}{\odot}}
\newcommand{\ncat}[1]{\nbin{#1}{\oplus}}
\newcommand{\nsum}[1]{\sum\limits_{\substack{#1}}}
\newcommand{\nfun}[2]{\mathop{\underset{\substack{#1}}{\namedtensorstrut\mathrm{#2}}}}
\newcommand{\ndef}[2]{\newcommand{#1}{\name{#2}}}
\newcommand{\nt}[1]{^{\transp(#1)}}
%
% Probability
\newcommand{\Normal}{\mathcal{N}}
\let\Pr\undefined
\DeclareMathOperator*{\Pr}{Pr}
\DeclareMathOperator*{\G}{\mathbb{G}}
\DeclareMathOperator*{\Odds}{Od}
\DeclareMathOperator*{\E}{E}
\DeclareMathOperator*{\Var}{Var}
\DeclareMathOperator*{\Cov}{Cov}
\DeclareMathOperator*{\corr}{corr}
\DeclareMathOperator*{\median}{median}
\newcommand{\dTV}{d_{\mathrm{TV}}}
\newcommand{\dHel}{d_{\mathrm{Hel}}}
\newcommand{\dJS}{d_{\mathrm{JS}}}
% ... information theory
\let\H\undefined
\DeclareMathOperator*{\H}{H}
\DeclareMathOperator*{\I}{I}
\DeclareMathOperator*{\D}{D}
%
%%% SPECIALIZED COMPUTER SCIENCE %%%
%
% Complexity classes
% .. classical
\newcommand{\Poly}{\mathsf{P}}
\newcommand{\NP}{\mathsf{NP}}
\newcommand{\PH}{\mathsf{PH}}
\newcommand{\PSPACE}{\mathsf{PSPACE}}
\renewcommand{\L}{\mathsf{L}}
% .. probabilistic
\newcommand{\formost}{\mathsf{Я}}
\newcommand{\RP}{\mathsf{RP}}
\newcommand{\BPP}{\mathsf{BPP}}
\newcommand{\MA}{\mathsf{MA}}
\newcommand{\AM}{\mathsf{AM}}
\newcommand{\IP}{\mathsf{IP}}
\newcommand{\RL}{\mathsf{RL}}
% .. circuits
\newcommand{\NC}{\mathsf{NC}}
\newcommand{\AC}{\mathsf{AC}}
\newcommand{\ACC}{\mathsf{ACC}}
\newcommand{\TC}{\mathsf{TC}}
\newcommand{\Ppoly}{\mathsf{P}/\poly}
\newcommand{\Lpoly}{\mathsf{L}/\poly}
% .. resources
\newcommand{\TIME}{\mathsf{TIME}}
\newcommand{\SPACE}{\mathsf{SPACE}}
\newcommand{\TISP}{\mathsf{TISP}}
\newcommand{\SIZE}{\mathsf{SIZE}}
% .. keywords
\newcommand{\co}{\mathsf{co}}
\newcommand{\Prom}{\mathsf{Promise}}
%
% Boolean analysis
\newcommand{\harpoon}{\!\upharpoonright\!}
\newcommand{\rr}[2]{#1\harpoon_{#2}}
\newcommand{\Fou}[1]{\widehat{#1}}
\DeclareMathOperator{\Ind}{\mathrm{Ind}}
\DeclareMathOperator{\Inf}{\mathrm{Inf}}
\DeclareMathOperator{\Der}{\mathrm{D}}
\DeclareMathOperator{\Stab}{\mathrm{Stab}}
\DeclareMathOperator{\T}{T}
\DeclareMathOperator{\sens}{\mathrm{s}}
\DeclareMathOperator{\bsens}{\mathrm{bs}}
\DeclareMathOperator{\fbsens}{\mathrm{fbs}}
\DeclareMathOperator{\Cert}{\mathrm{C}}
\DeclareMathOperator{\DT}{\mathrm{DT}}
\DeclareMathOperator{\CDT}{\mathrm{CDT}} % canonical
\DeclareMathOperator{\ECDT}{\mathrm{ECDT}}
\DeclareMathOperator{\CDTv}{\mathrm{CDT_{vars}}}
\DeclareMathOperator{\ECDTv}{\mathrm{ECDT_{vars}}}
\DeclareMathOperator{\CDTt}{\mathrm{CDT_{terms}}}
\DeclareMathOperator{\ECDTt}{\mathrm{ECDT_{terms}}}
\DeclareMathOperator{\CDTw}{\mathrm{CDT_{weighted}}}
\DeclareMathOperator{\ECDTw}{\mathrm{ECDT_{weighted}}}
\DeclareMathOperator{\AvgDT}{\mathrm{AvgDT}}
\DeclareMathOperator{\PDT}{\mathrm{PDT}} % partial decision tree
\DeclareMathOperator{\DTsize}{\mathrm{DT_{size}}}
\DeclareMathOperator{\W}{\mathbf{W}}
% .. functions (small caps sadly doesn't work)
\DeclareMathOperator{\Par}{\mathrm{Par}}
\DeclareMathOperator{\Maj}{\mathrm{Maj}}
\DeclareMathOperator{\HW}{\mathrm{HW}}
\DeclareMathOperator{\Th}{\mathrm{Th}}
\DeclareMathOperator{\Tribes}{\mathrm{Tribes}}
\DeclareMathOperator{\RotTribes}{\mathrm{RotTribes}}
\DeclareMathOperator{\CycleRun}{\mathrm{CycleRun}}
\DeclareMathOperator{\SAT}{\mathrm{SAT}}
\DeclareMathOperator{\UniqueSAT}{\mathrm{UniqueSAT}}
%
% Dynamic optimality
\newcommand{\OPT}{\mathsf{OPT}}
\newcommand{\Alt}{\mathsf{Alt}}
\newcommand{\Funnel}{\mathsf{Funnel}}
%
% Alignment
\DeclareMathOperator{\Amp}{\mathrm{Amp}}
%
%%% TYPESETTING %%%
%
% In text
\renewcommand{\th}{^{\mathrm{th}}}
\newcommand{\degree}{^\circ}
%
% Fonts
% .. bold
\newcommand{\BA}{\boldsymbol{A}}
\newcommand{\BB}{\boldsymbol{B}}
\newcommand{\BC}{\boldsymbol{C}}
\newcommand{\BD}{\boldsymbol{D}}
\newcommand{\BE}{\boldsymbol{E}}
\newcommand{\BF}{\boldsymbol{F}}
\newcommand{\BG}{\boldsymbol{G}}
\newcommand{\BH}{\boldsymbol{H}}
\newcommand{\BI}{\boldsymbol{I}}
\newcommand{\BJ}{\boldsymbol{J}}
\newcommand{\BK}{\boldsymbol{K}}
\newcommand{\BL}{\boldsymbol{L}}
\newcommand{\BM}{\boldsymbol{M}}
\newcommand{\BN}{\boldsymbol{N}}
\newcommand{\BO}{\boldsymbol{O}}
\newcommand{\BP}{\boldsymbol{P}}
\newcommand{\BQ}{\boldsymbol{Q}}
\newcommand{\BR}{\boldsymbol{R}}
\newcommand{\BS}{\boldsymbol{S}}
\newcommand{\BT}{\boldsymbol{T}}
\newcommand{\BU}{\boldsymbol{U}}
\newcommand{\BV}{\boldsymbol{V}}
\newcommand{\BW}{\boldsymbol{W}}
\newcommand{\BX}{\boldsymbol{X}}
\newcommand{\BY}{\boldsymbol{Y}}
\newcommand{\BZ}{\boldsymbol{Z}}
\newcommand{\Ba}{\boldsymbol{a}}
\newcommand{\Bb}{\boldsymbol{b}}
\newcommand{\Bc}{\boldsymbol{c}}
\newcommand{\Bd}{\boldsymbol{d}}
\newcommand{\Be}{\boldsymbol{e}}
\newcommand{\Bf}{\boldsymbol{f}}
\newcommand{\Bg}{\boldsymbol{g}}
\newcommand{\Bh}{\boldsymbol{h}}
\newcommand{\Bi}{\boldsymbol{i}}
\newcommand{\Bj}{\boldsymbol{j}}
\newcommand{\Bk}{\boldsymbol{k}}
\newcommand{\Bp}{\boldsymbol{p}}
\newcommand{\Bq}{\boldsymbol{q}}
\newcommand{\Br}{\boldsymbol{r}}
\newcommand{\Bs}{\boldsymbol{s}}
\newcommand{\Bt}{\boldsymbol{t}}
\newcommand{\Bu}{\boldsymbol{u}}
\newcommand{\Bv}{\boldsymbol{v}}
\newcommand{\Bw}{\boldsymbol{w}}
\newcommand{\Bx}{\boldsymbol{x}}
\newcommand{\By}{\boldsymbol{y}}
\newcommand{\Bz}{\boldsymbol{z}}
\newcommand{\Balpha}{\boldsymbol{\alpha}}
\newcommand{\Bbeta}{\boldsymbol{\beta}}
\newcommand{\Bgamma}{\boldsymbol{\gamma}}
\newcommand{\Bdelta}{\boldsymbol{\delta}}
\newcommand{\Beps}{\boldsymbol{\eps}}
\newcommand{\Bveps}{\boldsymbol{\veps}}
\newcommand{\Bzeta}{\boldsymbol{\zeta}}
\newcommand{\Beta}{\boldsymbol{\eta}}
\newcommand{\Btheta}{\boldsymbol{\theta}}
\newcommand{\Biota}{\boldsymbol{\iota}}
\newcommand{\Bkappa}{\boldsymbol{\kappa}}
\newcommand{\Blambda}{\boldsymbol{\lambda}}
\newcommand{\Bmu}{\boldsymbol{\mu}}
\newcommand{\Bnu}{\boldsymbol{\nu}}
\newcommand{\Bxi}{\boldsymbol{\xi}}
\newcommand{\Bomicron}{\boldsymbol{\omicron}}
\newcommand{\Bpi}{\boldsymbol{\pi}}
\newcommand{\Brho}{\boldsymbol{\rho}}
\newcommand{\Bsigma}{\boldsymbol{\sigma}}
\newcommand{\Btau}{\boldsymbol{\tau}}
\newcommand{\Bupsilon}{\boldsymbol{\upsilon}}
\newcommand{\Bphi}{\boldsymbol{\phi}}
\newcommand{\Bfi}{\boldsymbol{\fi}}
\newcommand{\Bchi}{\boldsymbol{\chi}}
\newcommand{\Bpsi}{\boldsymbol{\psi}}
\newcommand{\Bomega}{\boldsymbol{\omega}}
% .. calligraphic
\newcommand{\CA}{\mathcal{A}}
\newcommand{\CB}{\mathcal{B}}
\newcommand{\CC}{\mathcal{C}}
\newcommand{\CD}{\mathcal{D}}
\newcommand{\CE}{\mathcal{E}}
\newcommand{\CF}{\mathcal{F}}
\newcommand{\CG}{\mathcal{G}}
\newcommand{\CH}{\mathcal{H}}
\newcommand{\CI}{\mathcal{I}}
\newcommand{\CJ}{\mathcal{J}}
\newcommand{\CK}{\mathcal{K}}
\newcommand{\CL}{\mathcal{L}}
\newcommand{\CM}{\mathcal{M}}
\newcommand{\CN}{\mathcal{N}}
\newcommand{\CO}{\mathcal{O}}
\newcommand{\CP}{\mathcal{P}}
\newcommand{\CQ}{\mathcal{Q}}
\newcommand{\CR}{\mathcal{R}}
\newcommand{\CS}{\mathcal{S}}
\newcommand{\CT}{\mathcal{T}}
\newcommand{\CU}{\mathcal{U}}
\newcommand{\CV}{\mathcal{V}}
\newcommand{\CW}{\mathcal{W}}
\newcommand{\CX}{\mathcal{X}}
\newcommand{\CY}{\mathcal{Y}}
\newcommand{\CZ}{\mathcal{Z}}
% .. typewriter
\newcommand{\TA}{\mathtt{A}}
\newcommand{\TB}{\mathtt{B}}
\newcommand{\TC}{\mathtt{C}}
\newcommand{\TD}{\mathtt{D}}
\newcommand{\TE}{\mathtt{E}}
\newcommand{\TF}{\mathtt{F}}
\newcommand{\TG}{\mathtt{G}}
\newcommand{\TH}{\mathtt{H}}
\newcommand{\TI}{\mathtt{I}}
\newcommand{\TJ}{\mathtt{J}}
\newcommand{\TK}{\mathtt{K}}
\newcommand{\TL}{\mathtt{L}}
\newcommand{\TM}{\mathtt{M}}
\newcommand{\TN}{\mathtt{N}}
\newcommand{\TO}{\mathtt{O}}
\newcommand{\TP}{\mathtt{P}}
\newcommand{\TQ}{\mathtt{Q}}
\newcommand{\TR}{\mathtt{R}}
\newcommand{\TS}{\mathtt{S}}
\newcommand{\TT}{\mathtt{T}}
\newcommand{\TU}{\mathtt{U}}
\newcommand{\TV}{\mathtt{V}}
\newcommand{\TW}{\mathtt{W}}
\newcommand{\TX}{\mathtt{X}}
\newcommand{\TY}{\mathtt{Y}}
\newcommand{\TZ}{\mathtt{Z}}$
Adapted from lectures 10 and 11 of Ryan O’Donnell’s Fall 2017 graduate complexity theory class at CMU.
Randomness doesn’t seem all that powerful. To the extent that we believe (cryptographic) pseudorandom generators exist, we should believe that having access to randomness doesn’t help for decision problems: $\BPP = \Poly$.
On the other hand, with our current knowledge, if $\NP$ is like finding a needle in a haystack, then $\BPP$ is like trying to figure out whether there’s more hay or more needles: you can try to “get a rough idea” on the surface, but who’s to say that the inside of the stack isn’t all hay, or all needles? At least, in the case of $\NP$, when you do find a needle, you’re 100% sure the answer is “there is a needle”. $\RP$ is a randomized class that still has this property, since it has no “false positives”: it’s either mostly needles or all hay. But for $\BPP$, you can’t really be sure of the answer until you’ve counted almost everything; there’s no absolute guarantee.
This note is about getting absolute guarantees from probabilistic guarantees.
Magical advice strings: $\BPP \sse \Ppoly$
A language $L$ is in $\BPP$ if there is a “verifier” $V$ that will give the right answer most of the time: for say $90\%$ of values of a string $r \in \zo^s$ of random coin flips. We can express this as
\[\forall x \in \zo^n,\formost r \in \zo^s: V(x,r) = \One[x \in L],\]
where $\formost$ is a “for most” quantifier: “$\formost r: \text{blah}$” means “$\Pr_r[\text{blah}] \geq 90\%$” (with the understanding that the specific value $90\%$ is not going to matter).
By repeating this with $m=O(n)$ many draws of the random string $r$ and taking the majority answer, we can go from “most of the time” to probability say $\ge 1-4^{-n}$ (for simplicity, let’s keep denoting these $m$ random strings as a single string $r \in \zo^s$).
In itself, it doesn’t really help us: this is no absolute guarantee, because we could still get (very) unlucky and stumble upon the $4^{-n}$ fraction of random strings $r$ that give the wrong answer. But if we look at all possible input strings $x \in \zo^n$ of a certain length $n$, this $4^{-n}$ fraction is so small that only a $2^{-n}$ fraction of strings $r$ would give the wrong answer for any $x$. We have flipped the order of quantifiers from $\forall \formost$ to $\formost\forall$:
\[
\formost r \in \zo^s, \forall x \in \zo^n: V(x,r) = \One[x \in L].
\]
In particular, this means that for any input length $n$ there exists a single string $r^*$ that gives the right answer for all strings of that length. That is, if I could whisper that magical string $r^*$ in your ear, you could use it to get the right answer on any $x \in \zo^n$ with absolute certainty.
In complexity theory, “magical strings that you can use to get the right answer for all input strings of a certain length” are called “advice”, and this shows that $L \in \Ppoly$.
The art of squinting: $\BPP \sse \Sigma_2\Poly$
In the previous section, we only managed to get absolute guarantees with a little external advice. This time, let’s try to to this without help: find some test procedure which, for any $x$, can figure out whether $\Pr_{r \in \zo^s}[V(x,r)=1]$ is very large (say $\geq 1-2^{-n}$) or very small (say $\le 2^{-n}$). Let’s fix $x$ and look at what we have pictorially: if we look at the set $S \coloneqq \set{r \mid V(x,r)=1}$, it either covers almost all of the probability space $\zo^s$, or only a tiny fraction of it.
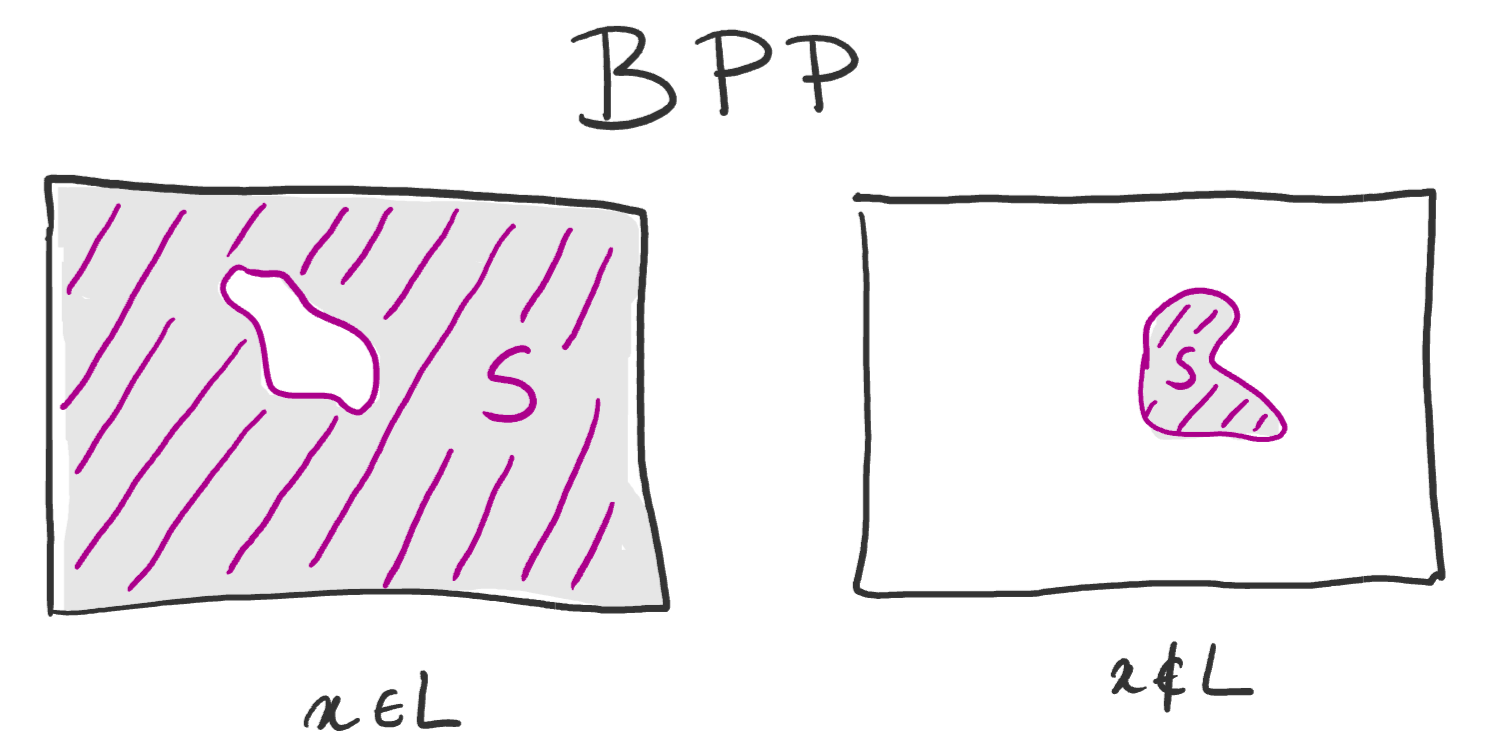
We would be very happy if we could reduce to a case where either the left drawing is completely full (and the right is not) or the right drawing is completely empty (and the left is not): this would respectively correspond to
- $\co\NP$: if you find an $r$ such that $V(x,r) = 0$, that’s a witness that $x \not\in L$;
- $\NP$: if you find an $r$ such that $V(x,r) = 1$, that’s a witness that $x \in L$.
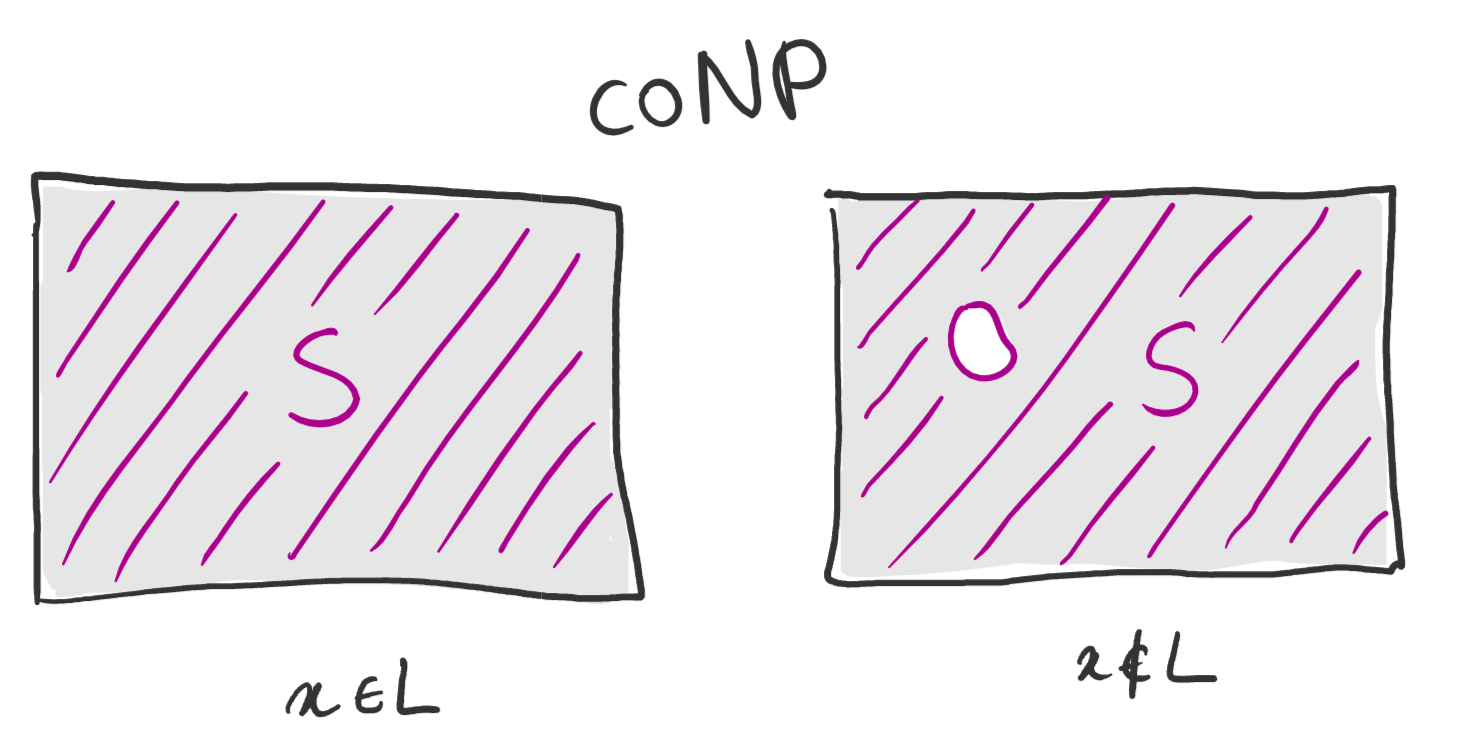
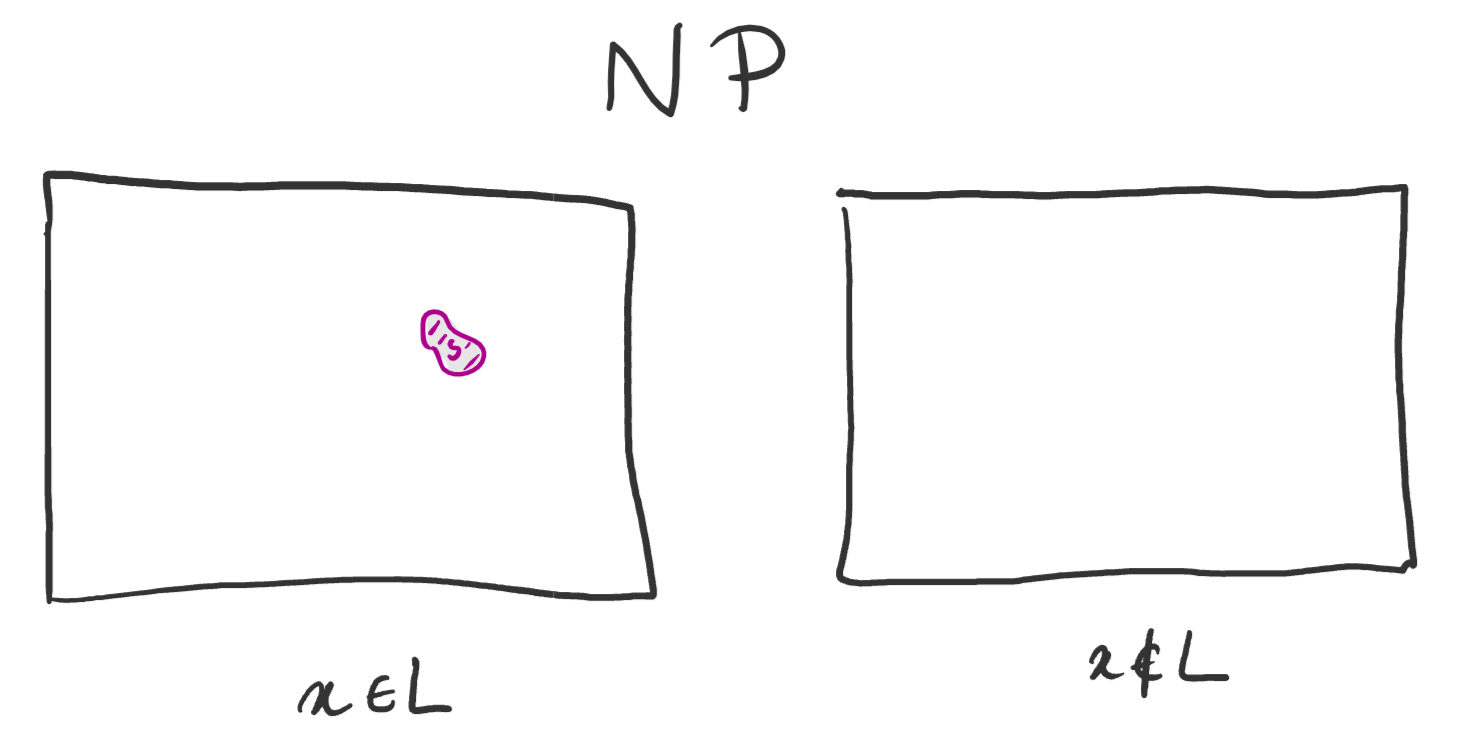
In fact, if you squint a bit, you might argue that the $\BPP$ picture looks a bit like the $\co\NP$ picture: at least the way we drew it, if we take two slightly offset copies of $S$ and stack them on top of each other, the left drawing becomes completely full, while the right drawing is still mostly empty ($S$ only grew by a factor two).
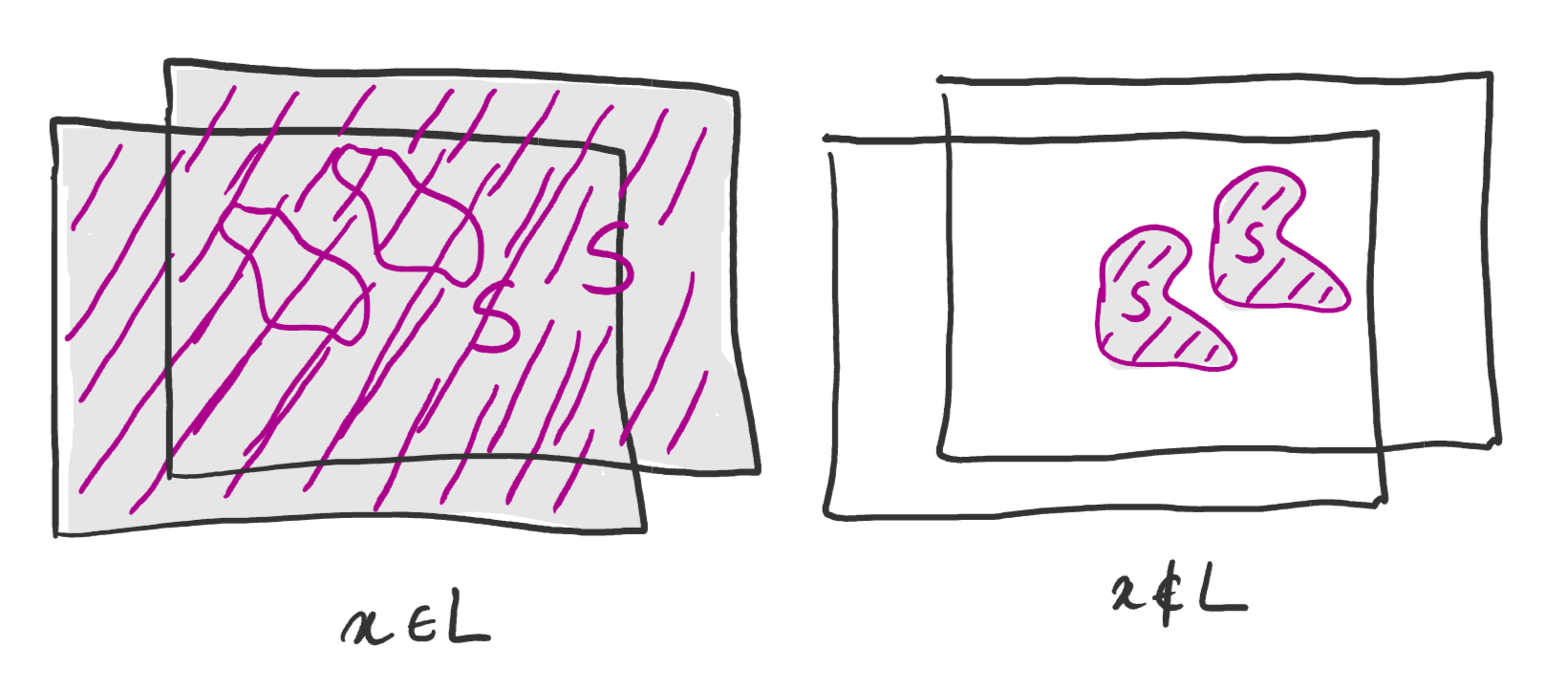
Does this trick always work? And what does it even mean to take an “offset copy” of $S$? We can define an “offset copy” using XOR: for any offset $d \in \zo^s$, we let $S \xor d \ce \set{r \xor d \mid r \in S}$. If whenever $x \in L$ we could always find a $d$ such that $S \union (S \xor d) = \zo^s$, then whatever random string $r$ you choose, you’d be guaranteed that either $r$ or $r \xor d$ is in $S$. On the other hand, when $x \not\in L$, $S$ is clearly too small for such a $d$ to exist: no matter what $d$ is, there will be some (in fact, most) values of $r$ for which neither $r$ nor $r \xor d$ is in $S$. This would be some concrete, absolute guarantee (though it involves some quantifiers)!
Unfortunately, there are extremely large sets $S$ for which it’s impossible to find a $d$ such that $S \union (S \xor d) = \zo^s$.
However, if we “squint many times” by taking the union of several offset copies of $S$, then we can cover all of $\zo^s$. Indeed, consider taking $s$ independently random offsets $d^{(1)}, \ldots, d^{(s)} \in \zo^s$. Then, the probability that some $r$ fails to be in $(S \xor d^{(1)}) \union \cdots \union (S \xor d^{(s)})$ is
\[\leq \p{1-\frac{|S|}{2^s}}^s \leq \p{2^{-n}}^s = 2^{-sn}.\]
Therefore, by a union bound over all $r \in \zo^s$, it will be overwhelmingly likely that $(S \xor d^{(1)}) \union \cdots \union (S \xor d^{(s)})$ covers all of $\zo^s$.
On the other hand, when $x \not\in L$, we have $S$ contains only a $2^{-n}$ fraction of the probability space, so no matter what happens, $(S \xor d^{(1)}) \union \cdots \union (S \xor d^{(s)})$ can only an $s\cdot 2^{-n}$ fraction, which is tiny (since $s$ is polynomial in $n$).
Since we can’t just enumerate over every possible value of those offsets $d^{(1)}, \ldots, d^{(s)}$, this doesn’t quite give us $L \in \co\NP$, but it gives us something. Concretely, we have
- when $x \in L$, then $\exists d^{(1)}, \ldots, d^{(s)} \in \zo^s$ such that $\forall r \in \zo^s$, at least one of the strings $r \xor d^{(i)}$ satisfy $V(x, r \xor d^{(i)})=1$;
- when $x \not\in L$, then $\forall d^{(1)}, \ldots, d^{(s)} \in \zo^s$, there will be some $r \in \set{0,1}^s$ such that none of the strings $r \xor d^{(i)}$ will satisfy $V(x, r \xor d^{(i)}) = 1$.
Since the test “is $V(x, r \xor d^{(i)}) = 1$ for any $i \in [s]$?” is a polynomial-time computation, this follows the definition of $\Sigma_2\Poly$.
What more can we do?
In a follow-up note, we explore these tricks further and generalize them to get a good number of corollaries, with a focus on Arthur-Merlin classes.