$\require{mathtools}
\newcommand{\nc}{\newcommand}
%
%%% GENERIC MATH %%%
%
% Environments
\newcommand{\al}[1]{\begin{align}#1\end{align}} % need this for \tag{} to work
\renewcommand{\r}{\mathrm}
\renewcommand{\t}{\textrm}
%
% Delimiters
% (I needed to create my own because the MathJax version of \DeclarePairedDelimiter doesn't have \mathopen{} and that messes up the spacing)
% .. one-part
\newcommand{\p}[1]{\mathopen{}\left( #1 \right)}
\renewcommand{\P}[1]{^{\p{#1}}}
\renewcommand{\b}[1]{\mathopen{}\left[ #1 \right]}
\newcommand{\set}[1]{\mathopen{}\left\{ #1 \right\}}
\newcommand{\abs}[1]{\mathopen{}\left\lvert #1 \right\rvert}
\newcommand{\floor}[1]{\mathopen{}\left\lfloor #1 \right\rfloor}
\newcommand{\ceil}[1]{\mathopen{}\left\lceil #1 \right\rceil}
\newcommand{\inner}[1]{\mathopen{}\left\langle #1 \right\rangle}
\newcommand{\norm}[1]{\mathopen{}\left\lVert #1 \strut \right\rVert}
\newcommand{\frob}[1]{\norm{#1}_\mathrm{F}}
\newcommand{\mix}[1]{\mathopen{}\left\lfloor #1 \right\rceil}
%% .. two-part
\newcommand{\inco}[2]{#1 \mathop{}\middle|\mathop{} #2}
\newcommand{\co}[2]{ {\left.\inco{#1}{#2}\right.}}
\newcommand{\cond}{\co} % deprecated
\newcommand{\pco}[2]{\p{\inco{#1}{#2}}}
\newcommand{\bco}[2]{\b{\inco{#1}{#2}}}
\newcommand{\setco}[2]{\set{\inco{#1}{#2}}}
\newcommand{\at}[2]{ {\left.#1\strut\right|_{#2}}}
\newcommand{\pat}[2]{\p{\at{#1}{#2}}}
\newcommand{\bat}[2]{\b{\at{#1}{#2}}}
\newcommand{\para}[2]{#1\strut \mathop{}\middle\|\mathop{} #2}
\newcommand{\ppa}[2]{\p{\para{#1}{#2}}}
\newcommand{\pff}[2]{\p{\ff{#1}{#2}}}
\newcommand{\bff}[2]{\b{\ff{#1}{#2}}}
\newcommand{\bffco}[4]{\bff{\cond{#1}{#2}}{\cond{#3}{#4}}}
\newcommand{\sm}[1]{\p{\begin{smallmatrix}#1\end{smallmatrix}}}
%
% Greek
\newcommand{\eps}{\epsilon}
\newcommand{\veps}{\varepsilon}
\newcommand{\vpi}{\varpi}
% the following cause issues with real LaTeX tho :/ maybe consider naming it \fhi instead?
\let\fi\phi % because it looks like an f
\let\phi\varphi % because it looks like a p
\renewcommand{\th}{\theta}
\newcommand{\Th}{\Theta}
\newcommand{\om}{\omega}
\newcommand{\Om}{\Omega}
%
% Miscellaneous
\newcommand{\LHS}{\mathrm{LHS}}
\newcommand{\RHS}{\mathrm{RHS}}
\DeclareMathOperator{\cst}{const}
% .. operators
\DeclareMathOperator{\poly}{poly}
\DeclareMathOperator{\polylog}{polylog}
\DeclareMathOperator{\quasipoly}{quasipoly}
\DeclareMathOperator{\negl}{negl}
\DeclareMathOperator*{\argmin}{arg\thinspace min}
\DeclareMathOperator*{\argmax}{arg\thinspace max}
% .. functions
\DeclareMathOperator{\id}{id}
\DeclareMathOperator{\sign}{sign}
\DeclareMathOperator{\err}{err}
\DeclareMathOperator{\ReLU}{ReLU}
% .. analysis
\let\d\undefined
\newcommand{\d}{\operatorname{d}\mathopen{}}
\newcommand{\dd}[1]{\operatorname{d}^{#1}\mathopen{}}
\newcommand{\df}[2]{ {\f{\d #1}{\d #2}}}
\newcommand{\ds}[2]{ {\sl{\d #1}{\d #2}}}
\newcommand{\ddf}[3]{ {\f{\dd{#1} #2}{\p{\d #3}^{#1}}}}
\newcommand{\dds}[3]{ {\sl{\dd{#1} #2}{\p{\d #3}^{#1}}}}
\renewcommand{\part}{\partial}
\newcommand{\partf}[2]{\f{\part #1}{\part #2}}
\newcommand{\parts}[2]{\sl{\part #1}{\part #2}}
\newcommand{\grad}[1]{\mathop{\nabla\!_{#1}}}
% .. sets
\newcommand{\es}{\emptyset}
\newcommand{\N}{\mathbb{N}}
\newcommand{\Z}{\mathbb{Z}}
\newcommand{\R}{\mathbb{R}}
\newcommand{\C}{\mathbb{C}}
\newcommand{\F}{\mathbb{F}}
\newcommand{\zo}{\set{0,1}}
\newcommand{\pmo}{\set{\pm 1}}
\newcommand{\zpmo}{\set{0,\pm 1}}
% .... set operations
\newcommand{\sse}{\subseteq}
\newcommand{\out}{\not\in}
\newcommand{\minus}{\setminus}
\newcommand{\inc}[1]{\union \set{#1}} % "including"
\newcommand{\exc}[1]{\setminus \set{#1}} % "except"
% .. over and under
\renewcommand{\ss}[1]{_{\substack{#1}}}
\newcommand{\OB}{\overbrace}
\newcommand{\ob}[2]{\OB{#1}^\t{#2}}
\newcommand{\UB}{\underbrace}
\newcommand{\ub}[2]{\UB{#1}_\t{#2}}
\newcommand{\ol}{\overline}
\newcommand{\tld}{\widetilde} % deprecated
\renewcommand{\~}{\widetilde}
\newcommand{\HAT}{\widehat} % deprecated
\renewcommand{\^}{\widehat}
\newcommand{\rt}[1]{ {\sqrt{#1}}}
\newcommand{\for}[2]{_{#1=1}^{#2}}
\newcommand{\sfor}{\sum\for}
\newcommand{\pfor}{\prod\for}
% .... two-part
\newcommand{\f}{\frac}
\renewcommand{\sl}[2]{#1 /\mathopen{}#2}
\newcommand{\ff}[2]{\mathchoice{\begin{smallmatrix}\displaystyle\vphantom{\p{#1}}#1\\[-0.05em]\hline\\[-0.05em]\hline\displaystyle\vphantom{\p{#2}}#2\end{smallmatrix}}{\begin{smallmatrix}\vphantom{\p{#1}}#1\\[-0.1em]\hline\\[-0.1em]\hline\vphantom{\p{#2}}#2\end{smallmatrix}}{\begin{smallmatrix}\vphantom{\p{#1}}#1\\[-0.1em]\hline\\[-0.1em]\hline\vphantom{\p{#2}}#2\end{smallmatrix}}{\begin{smallmatrix}\vphantom{\p{#1}}#1\\[-0.1em]\hline\\[-0.1em]\hline\vphantom{\p{#2}}#2\end{smallmatrix}}}
% .. arrows
\newcommand{\from}{\leftarrow}
\DeclareMathOperator*{\<}{\!\;\longleftarrow\;\!}
\let\>\undefined
\DeclareMathOperator*{\>}{\!\;\longrightarrow\;\!}
\let\-\undefined
\DeclareMathOperator*{\-}{\!\;\longleftrightarrow\;\!}
\newcommand{\so}{\implies}
% .. operators and relations
\renewcommand{\*}{\cdot}
\newcommand{\x}{\times}
\newcommand{\sr}{\stackrel}
\newcommand{\ce}{\coloneqq}
\newcommand{\ec}{\eqqcolon}
\newcommand{\ap}{\approx}
\newcommand{\ls}{\lesssim}
\newcommand{\gs}{\gtrsim}
% .. punctuation and spacing
\renewcommand{\.}[1]{#1\dots#1}
\newcommand{\ts}{\thinspace}
\newcommand{\q}{\quad}
\newcommand{\qq}{\qquad}
%
% Levels of closeness
\newcommand{\scirc}[1]{\sr{\circ}{#1}}
\newcommand{\sdot}[1]{\sr{.}{#1}}
\newcommand{\slog}[1]{\sr{\log}{#1}}
\newcommand{\createClosenessLevels}[7]{
\newcommand{#2}{\mathrel{(#1)}}
\newcommand{#3}{\mathrel{#1}}
\newcommand{#4}{\mathrel{#1\!\!#1}}
\newcommand{#5}{\mathrel{#1\!\!#1\!\!#1}}
\newcommand{#6}{\mathrel{(\sdot{#1})}}
\newcommand{#7}{\mathrel{(\slog{#1})}}
}
\let\lt\undefined
\let\gt\undefined
% .. vanilla versions (is it within a constant?)
\newcommand{\ez}{\scirc=}
\newcommand{\eq}{\simeq}
\newcommand{\eqq}{\mathrel{\eq\!\!\eq}}
\newcommand{\eqqq}{\mathrel{\eq\!\!\eq\!\!\eq}}
\newcommand{\lez}{\scirc\le}
\renewcommand{\lq}{\preceq}
\newcommand{\lqq}{\mathrel{\lq\!\!\lq}}
\newcommand{\lqqq}{\mathrel{\lq\!\!\lq\!\!\lq}}
\newcommand{\gez}{\scirc\ge}
\newcommand{\gq}{\succeq}
\newcommand{\gqq}{\mathrel{\gq\!\!\gq}}
\newcommand{\gqqq}{\mathrel{\gq\!\!\gq\!\!\gq}}
\newcommand{\lz}{\scirc<}
\newcommand{\lt}{\prec}
\newcommand{\ltt}{\mathrel{\lt\!\!\lt}}
\newcommand{\lttt}{\mathrel{\lt\!\!\lt\!\!\lt}}
\newcommand{\gz}{\scirc>}
\newcommand{\gt}{\succ}
\newcommand{\gtt}{\mathrel{\gt\!\!\gt}}
\newcommand{\gttt}{\mathrel{\gt\!\!\gt\!\!\gt}}
% .. dotted versions (is it equal in the limit?)
\newcommand{\ed}{\sdot=}
\newcommand{\eqd}{\sdot\eq}
\newcommand{\eqqd}{\sdot\eqq}
\newcommand{\eqqqd}{\sdot\eqqq}
\newcommand{\led}{\sdot\le}
\newcommand{\lqd}{\sdot\lq}
\newcommand{\lqqd}{\sdot\lqq}
\newcommand{\lqqqd}{\sdot\lqqq}
\newcommand{\ged}{\sdot\ge}
\newcommand{\gqd}{\sdot\gq}
\newcommand{\gqqd}{\sdot\gqq}
\newcommand{\gqqqd}{\sdot\gqqq}
\newcommand{\ld}{\sdot<}
\newcommand{\ltd}{\sdot\lt}
\newcommand{\lttd}{\sdot\ltt}
\newcommand{\ltttd}{\sdot\lttt}
\newcommand{\gd}{\sdot>}
\newcommand{\gtd}{\sdot\gt}
\newcommand{\gttd}{\sdot\gtt}
\newcommand{\gtttd}{\sdot\gttt}
% .. log versions (is it equal up to log?)
\newcommand{\elog}{\slog=}
\newcommand{\eqlog}{\slog\eq}
\newcommand{\eqqlog}{\slog\eqq}
\newcommand{\eqqqlog}{\slog\eqqq}
\newcommand{\lelog}{\slog\le}
\newcommand{\lqlog}{\slog\lq}
\newcommand{\lqqlog}{\slog\lqq}
\newcommand{\lqqqlog}{\slog\lqqq}
\newcommand{\gelog}{\slog\ge}
\newcommand{\gqlog}{\slog\gq}
\newcommand{\gqqlog}{\slog\gqq}
\newcommand{\gqqqlog}{\slog\gqqq}
\newcommand{\llog}{\slog<}
\newcommand{\ltlog}{\slog\lt}
\newcommand{\lttlog}{\slog\ltt}
\newcommand{\ltttlog}{\slog\lttt}
\newcommand{\glog}{\slog>}
\newcommand{\gtlog}{\slog\gt}
\newcommand{\gttlog}{\slog\gtt}
\newcommand{\gtttlog}{\slog\gttt}
%
%
%%% SPECIALIZED MATH %%%
%
% Logic and bit operations
\newcommand{\fa}{\forall}
\newcommand{\ex}{\exists}
\renewcommand{\and}{\wedge}
\newcommand{\AND}{\bigwedge}
\renewcommand{\or}{\vee}
\newcommand{\OR}{\bigvee}
\newcommand{\xor}{\oplus}
\newcommand{\XOR}{\bigoplus}
\newcommand{\union}{\cup}
\newcommand{\inter}{\cap}
\newcommand{\UNION}{\bigcup}
\newcommand{\INTER}{\bigcap}
\newcommand{\comp}{\overline}
\newcommand{\true}{\r{true}}
\newcommand{\false}{\r{false}}
\newcommand{\tf}{\set{\true,\false}}
\DeclareMathOperator{\One}{\mathbb{1}}
\DeclareMathOperator{\1}{\mathbb{1}} % use \mathbbm instead if using real LaTeX
\DeclareMathOperator{\LSB}{LSB}
%
% Linear algebra
\newcommand{\spn}{\mathrm{span}} % do NOT use \span because it causes misery with amsmath
\DeclareMathOperator{\rank}{rank}
\DeclareMathOperator{\proj}{proj}
\DeclareMathOperator{\dom}{dom}
\DeclareMathOperator{\Img}{Im}
\newcommand{\transp}{\mathsf{T}}
\newcommand{\T}{^\transp}
% .. named tensors
\newcommand{\namedtensorstrut}{\vphantom{fg}} % milder than \mathstrut
\newcommand{\name}[1]{\mathsf{\namedtensorstrut #1}}
\newcommand{\nbin}[2]{\mathbin{\underset{\substack{#1}}{\namedtensorstrut #2}}}
\newcommand{\ndot}[1]{\nbin{#1}{\odot}}
\newcommand{\ncat}[1]{\nbin{#1}{\oplus}}
\newcommand{\nsum}[1]{\sum\limits_{\substack{#1}}}
\newcommand{\nfun}[2]{\mathop{\underset{\substack{#1}}{\namedtensorstrut\mathrm{#2}}}}
\newcommand{\ndef}[2]{\newcommand{#1}{\name{#2}}}
\newcommand{\nt}[1]{^{\transp(#1)}}
%
% Probability
\newcommand{\tri}{\triangle}
\newcommand{\Normal}{\mathcal{N}}
% .. operators
\DeclareMathOperator{\supp}{supp}
\let\Pr\undefined
\DeclareMathOperator*{\Pr}{Pr}
\DeclareMathOperator*{\G}{\mathbb{G}}
\DeclareMathOperator*{\Odds}{Od}
\DeclareMathOperator*{\E}{E}
\DeclareMathOperator*{\Var}{Var}
\DeclareMathOperator*{\Cov}{Cov}
\DeclareMathOperator*{\K}{K}
\DeclareMathOperator*{\corr}{corr}
\DeclareMathOperator*{\median}{median}
\DeclareMathOperator*{\maj}{maj}
% ... information theory
\let\H\undefined
\DeclareMathOperator*{\H}{H}
\DeclareMathOperator*{\I}{I}
\DeclareMathOperator*{\D}{D}
\DeclareMathOperator*{\KL}{KL}
% .. other divergences
\newcommand{\dTV}{d_{\mathrm{TV}}}
\newcommand{\dHel}{d_{\mathrm{Hel}}}
\newcommand{\dJS}{d_{\mathrm{JS}}}
%
%%% SPECIALIZED COMPUTER SCIENCE %%%
%
% Complexity classes
% .. classical
\newcommand{\Poly}{\mathsf{P}}
\newcommand{\NP}{\mathsf{NP}}
\newcommand{\PH}{\mathsf{PH}}
\newcommand{\PSPACE}{\mathsf{PSPACE}}
\renewcommand{\L}{\mathsf{L}}
% .. probabilistic
\newcommand{\formost}{\mathsf{Я}}
\newcommand{\RP}{\mathsf{RP}}
\newcommand{\BPP}{\mathsf{BPP}}
\newcommand{\MA}{\mathsf{MA}}
\newcommand{\AM}{\mathsf{AM}}
\newcommand{\IP}{\mathsf{IP}}
\newcommand{\RL}{\mathsf{RL}}
% .. circuits
\newcommand{\NC}{\mathsf{NC}}
\newcommand{\AC}{\mathsf{AC}}
\newcommand{\ACC}{\mathsf{ACC}}
\newcommand{\ThrC}{\mathsf{TC}}
\newcommand{\Ppoly}{\mathsf{P}/\poly}
\newcommand{\Lpoly}{\mathsf{L}/\poly}
% .. resources
\newcommand{\TIME}{\mathsf{TIME}}
\newcommand{\SPACE}{\mathsf{SPACE}}
\newcommand{\TISP}{\mathsf{TISP}}
\newcommand{\SIZE}{\mathsf{SIZE}}
% .. keywords
\newcommand{\coclass}{\mathsf{co}}
\newcommand{\Prom}{\mathsf{Promise}}
%
% Boolean analysis
\newcommand{\harpoon}{\!\upharpoonright\!}
\newcommand{\rr}[2]{#1\harpoon_{#2}}
\newcommand{\Fou}[1]{\widehat{#1}}
\DeclareMathOperator{\Ind}{\mathrm{Ind}}
\DeclareMathOperator{\Inf}{\mathrm{Inf}}
\newcommand{\Der}[1]{\operatorname{D}_{#1}\mathopen{}}
\newcommand{\Exp}[1]{\operatorname{E}_{#1}\mathopen{}}
\DeclareMathOperator{\Stab}{\mathrm{Stab}}
\DeclareMathOperator{\Tau}{T}
\DeclareMathOperator{\sens}{\mathrm{s}}
\DeclareMathOperator{\bsens}{\mathrm{bs}}
\DeclareMathOperator{\fbsens}{\mathrm{fbs}}
\DeclareMathOperator{\Cert}{\mathrm{C}}
\DeclareMathOperator{\DT}{\mathrm{DT}}
\DeclareMathOperator{\CDT}{\mathrm{CDT}} % canonical
\DeclareMathOperator{\ECDT}{\mathrm{ECDT}}
\DeclareMathOperator{\CDTv}{\mathrm{CDT_{vars}}}
\DeclareMathOperator{\ECDTv}{\mathrm{ECDT_{vars}}}
\DeclareMathOperator{\CDTt}{\mathrm{CDT_{terms}}}
\DeclareMathOperator{\ECDTt}{\mathrm{ECDT_{terms}}}
\DeclareMathOperator{\CDTw}{\mathrm{CDT_{weighted}}}
\DeclareMathOperator{\ECDTw}{\mathrm{ECDT_{weighted}}}
\DeclareMathOperator{\AvgDT}{\mathrm{AvgDT}}
\DeclareMathOperator{\PDT}{\mathrm{PDT}} % partial decision tree
\DeclareMathOperator{\DTsize}{\mathrm{DT_{size}}}
\DeclareMathOperator{\W}{\mathbf{W}}
% .. functions (small caps sadly doesn't work)
\DeclareMathOperator{\Par}{\mathrm{Par}}
\DeclareMathOperator{\Maj}{\mathrm{Maj}}
\DeclareMathOperator{\HW}{\mathrm{HW}}
\DeclareMathOperator{\Thr}{\mathrm{Thr}}
\DeclareMathOperator{\Tribes}{\mathrm{Tribes}}
\DeclareMathOperator{\RotTribes}{\mathrm{RotTribes}}
\DeclareMathOperator{\CycleRun}{\mathrm{CycleRun}}
\DeclareMathOperator{\SAT}{\mathrm{SAT}}
\DeclareMathOperator{\UniqueSAT}{\mathrm{UniqueSAT}}
%
% Dynamic optimality
\newcommand{\OPT}{\mathsf{OPT}}
\newcommand{\Alt}{\mathsf{Alt}}
\newcommand{\Funnel}{\mathsf{Funnel}}
%
% Alignment
\DeclareMathOperator{\Amp}{\mathrm{Amp}}
%
%%% TYPESETTING %%%
%
% In "text"
\newcommand{\heart}{\heartsuit}
\newcommand{\nth}{^\t{th}}
\newcommand{\degree}{^\circ}
\newcommand{\qu}[1]{\text{``}#1\text{''}}
% remove these last two if using real LaTeX
\newcommand{\qed}{\blacksquare}
\newcommand{\qedhere}{\tag*{$\blacksquare$}}
%
% Fonts
% .. bold
\newcommand{\BA}{\boldsymbol{A}}
\newcommand{\BB}{\boldsymbol{B}}
\newcommand{\BC}{\boldsymbol{C}}
\newcommand{\BD}{\boldsymbol{D}}
\newcommand{\BE}{\boldsymbol{E}}
\newcommand{\BF}{\boldsymbol{F}}
\newcommand{\BG}{\boldsymbol{G}}
\newcommand{\BH}{\boldsymbol{H}}
\newcommand{\BI}{\boldsymbol{I}}
\newcommand{\BJ}{\boldsymbol{J}}
\newcommand{\BK}{\boldsymbol{K}}
\newcommand{\BL}{\boldsymbol{L}}
\newcommand{\BM}{\boldsymbol{M}}
\newcommand{\BN}{\boldsymbol{N}}
\newcommand{\BO}{\boldsymbol{O}}
\newcommand{\BP}{\boldsymbol{P}}
\newcommand{\BQ}{\boldsymbol{Q}}
\newcommand{\BR}{\boldsymbol{R}}
\newcommand{\BS}{\boldsymbol{S}}
\newcommand{\BT}{\boldsymbol{T}}
\newcommand{\BU}{\boldsymbol{U}}
\newcommand{\BV}{\boldsymbol{V}}
\newcommand{\BW}{\boldsymbol{W}}
\newcommand{\BX}{\boldsymbol{X}}
\newcommand{\BY}{\boldsymbol{Y}}
\newcommand{\BZ}{\boldsymbol{Z}}
\newcommand{\Ba}{\boldsymbol{a}}
\newcommand{\Bb}{\boldsymbol{b}}
\newcommand{\Bc}{\boldsymbol{c}}
\newcommand{\Bd}{\boldsymbol{d}}
\newcommand{\Be}{\boldsymbol{e}}
\newcommand{\Bf}{\boldsymbol{f}}
\newcommand{\Bg}{\boldsymbol{g}}
\newcommand{\Bh}{\boldsymbol{h}}
\newcommand{\Bi}{\boldsymbol{i}}
\newcommand{\Bj}{\boldsymbol{j}}
\newcommand{\Bk}{\boldsymbol{k}}
\newcommand{\Bl}{\boldsymbol{l}}
\newcommand{\Bm}{\boldsymbol{m}}
\newcommand{\Bn}{\boldsymbol{n}}
\newcommand{\Bo}{\boldsymbol{o}}
\newcommand{\Bp}{\boldsymbol{p}}
\newcommand{\Bq}{\boldsymbol{q}}
\newcommand{\Br}{\boldsymbol{r}}
\newcommand{\Bs}{\boldsymbol{s}}
\newcommand{\Bt}{\boldsymbol{t}}
\newcommand{\Bu}{\boldsymbol{u}}
\newcommand{\Bv}{\boldsymbol{v}}
\newcommand{\Bw}{\boldsymbol{w}}
\newcommand{\Bx}{\boldsymbol{x}}
\newcommand{\By}{\boldsymbol{y}}
\newcommand{\Bz}{\boldsymbol{z}}
\newcommand{\Balpha}{\boldsymbol{\alpha}}
\newcommand{\Bbeta}{\boldsymbol{\beta}}
\newcommand{\Bgamma}{\boldsymbol{\gamma}}
\newcommand{\Bdelta}{\boldsymbol{\delta}}
\newcommand{\Beps}{\boldsymbol{\eps}}
\newcommand{\Bveps}{\boldsymbol{\veps}}
\newcommand{\Bzeta}{\boldsymbol{\zeta}}
\newcommand{\Beta}{\boldsymbol{\eta}}
\newcommand{\Btheta}{\boldsymbol{\theta}}
\newcommand{\Bth}{\boldsymbol{\th}}
\newcommand{\Biota}{\boldsymbol{\iota}}
\newcommand{\Bkappa}{\boldsymbol{\kappa}}
\newcommand{\Blambda}{\boldsymbol{\lambda}}
\newcommand{\Bmu}{\boldsymbol{\mu}}
\newcommand{\Bnu}{\boldsymbol{\nu}}
\newcommand{\Bxi}{\boldsymbol{\xi}}
\newcommand{\Bpi}{\boldsymbol{\pi}}
\newcommand{\Bvpi}{\boldsymbol{\vpi}}
\newcommand{\Brho}{\boldsymbol{\rho}}
\newcommand{\Bsigma}{\boldsymbol{\sigma}}
\newcommand{\Btau}{\boldsymbol{\tau}}
\newcommand{\Bupsilon}{\boldsymbol{\upsilon}}
\newcommand{\Bphi}{\boldsymbol{\phi}}
\newcommand{\Bfi}{\boldsymbol{\fi}}
\newcommand{\Bchi}{\boldsymbol{\chi}}
\newcommand{\Bpsi}{\boldsymbol{\psi}}
\newcommand{\Bom}{\boldsymbol{\om}}
% .. calligraphic
\newcommand{\CA}{\mathcal{A}}
\newcommand{\CB}{\mathcal{B}}
\newcommand{\CC}{\mathcal{C}}
\newcommand{\CD}{\mathcal{D}}
\newcommand{\CE}{\mathcal{E}}
\newcommand{\CF}{\mathcal{F}}
\newcommand{\CG}{\mathcal{G}}
\newcommand{\CH}{\mathcal{H}}
\newcommand{\CI}{\mathcal{I}}
\newcommand{\CJ}{\mathcal{J}}
\newcommand{\CK}{\mathcal{K}}
\newcommand{\CL}{\mathcal{L}}
\newcommand{\CM}{\mathcal{M}}
\newcommand{\CN}{\mathcal{N}}
\newcommand{\CO}{\mathcal{O}}
\newcommand{\CP}{\mathcal{P}}
\newcommand{\CQ}{\mathcal{Q}}
\newcommand{\CR}{\mathcal{R}}
\newcommand{\CS}{\mathcal{S}}
\newcommand{\CT}{\mathcal{T}}
\newcommand{\CU}{\mathcal{U}}
\newcommand{\CV}{\mathcal{V}}
\newcommand{\CW}{\mathcal{W}}
\newcommand{\CX}{\mathcal{X}}
\newcommand{\CY}{\mathcal{Y}}
\newcommand{\CZ}{\mathcal{Z}}
% .. typewriter
\newcommand{\TA}{\mathtt{A}}
\newcommand{\TB}{\mathtt{B}}
\newcommand{\TC}{\mathtt{C}}
\newcommand{\TD}{\mathtt{D}}
\newcommand{\TE}{\mathtt{E}}
\newcommand{\TF}{\mathtt{F}}
\newcommand{\TG}{\mathtt{G}}
\renewcommand{\TH}{\mathtt{H}}
\newcommand{\TI}{\mathtt{I}}
\newcommand{\TJ}{\mathtt{J}}
\newcommand{\TK}{\mathtt{K}}
\newcommand{\TL}{\mathtt{L}}
\newcommand{\TM}{\mathtt{M}}
\newcommand{\TN}{\mathtt{N}}
\newcommand{\TO}{\mathtt{O}}
\newcommand{\TP}{\mathtt{P}}
\newcommand{\TQ}{\mathtt{Q}}
\newcommand{\TR}{\mathtt{R}}
\newcommand{\TS}{\mathtt{S}}
\newcommand{\TT}{\mathtt{T}}
\newcommand{\TU}{\mathtt{U}}
\newcommand{\TV}{\mathtt{V}}
\newcommand{\TW}{\mathtt{W}}
\newcommand{\TX}{\mathtt{X}}
\newcommand{\TY}{\mathtt{Y}}
\newcommand{\TZ}{\mathtt{Z}}$
Personal summary of Exact solutions to the nonlinear dynamics of learning in deep linear neural networks.
This paper shows you can decompose learning dynamics of a fully linear network into some (mostly independent) singular modes that learn at different rates (depending on the eigenvalues of the input-output correlation matrix). In fact, it’s as if the network is “simulating” another network for which the correlation between input and output coordinates is diagonal.
General setup
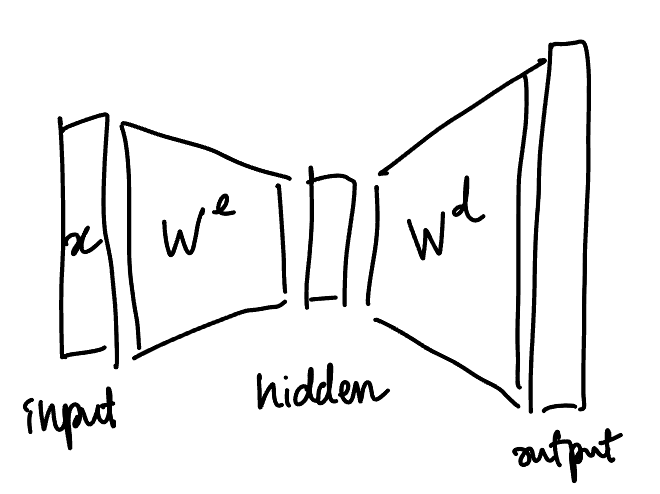
The model is $\ndef{\input}{input}\ndef{\hidden}{hidden}\ndef{\output}{output}\ndef{\data}{data}\newcommand{\We}{W^\mathrm{e}}\newcommand{\Wd}{W^\mathrm{d}}x\ndot\input\We\ndot\hidden \Wd$ (using named tensor notation), where
- $\We \in \R^{\input \times \hidden}$ “encodes” the input $x$ into a hidden layer,
- $\Wd \in \R^{\hidden\times \output}$ “decodes” the hidden layer into the output,
and both $\We$ and $\Wd$ are initialized as independent Gaussians.
It is trained on $N$ data points:
- inputs: $X \ce (x^{(1)}, \ldots, x^{(n)}) \in \R^{\data \times \input}$,
- outputs: $Y \ce (y^{(1)}, \cdots, y^{(n)}) \in \R^{\data \times \output}$.
Which means the square loss is
\[
\CL
%\ce \sum_{d=1}^D \norm{y^{(d)}-\Wd \ndot\hidden \We\ndot\input x^{(d)}}_\output^2
\ce \sum_\data\norm{Y - X \ndot\input \We\ndot\hidden \Wd}_\output^2.
\]
Taking the differential, we get
\[
\al{
\partial \CL
&= \sum_\data 2 \p{Y - X \ndot\input \We\ndot\hidden \Wd}\ndot\output\partial\p{Y - X \ndot\input \We\ndot\hidden \Wd}\\
&= -2 \sum_\data \p{Y - X \ndot\input \We\ndot\hidden \Wd}\ndot\output\b{X\ndot\input\p{\partial\We \ndot\hidden \Wd + \We \ndot\hidden \partial\Wd}}\\
&= -2 \b{X\ndot\data\p{Y - X \ndot\input \We\ndot\hidden \Wd} } \ndot{\input\\\output}\p{\partial\We \ndot\hidden \Wd + \We \ndot\hidden \partial\Wd}.
}
\]
Let’s assume that $X \ndot\data X = I_\input$ (i.e. the input coordinates have been standardized to have mean $0$, variance $1$ and be uncorrelated). Then we have
\[
%\CE =
X\ndot\data\p{Y - X \ndot\input \We\ndot\hidden \Wd} = \UB{X\ndot\data Y}_{\ec\ \Sigma} - \We \ndot\hidden \Wd,
\]
where the “input-output correlations” matrix $\Sigma \ce X \ndot\data Y \in \R^{\input \times \output}$ completely captures the problem. The matrix product $\We \ndot\hidden \Wd$ is “trying” to match these correlations $\Sigma$, and the learning dynamics are given by
\[
\al{
\frac{\d\We}{\d t} = -\frac{\partial\CL}{\partial\We} &= 2\p{\Sigma - \We\ndot\hidden\Wd}\ndot\output\Wd\\
\frac{\d\Wd}{\d t} = -\frac{\partial\CL}{\partial\Wd} &= 2\p{\Sigma - \We\ndot\hidden\Wd}\ndot\input\We.
}
\]
We’ll drop those factors $2$ for simplicity.
Diagonal case
Suppose that $|\input| = |\output|\ec d$, and that $\Sigma$ is diagonal with elements $s_1, \ldots, s_n$. Then we can decompose the dynamics into (somewhat) independent parts if we group the weights by which input/output coordinate they connect to:
\[
\al{
\frac{\d\We_{\input(i)}}{\d t} &= \p{s_i - \We_{\input(i)}\ndot\hidden\Wd_{\output(i)}}\Wd_{\output(i)} - \sum_{j \ne i} \p{\We_{\input(i)}\ndot\hidden\Wd_{\output(j)}}\Wd_{\output(j)}\\
\frac{\d\Wd_{\output(i)}}{\d t} &= \UB{\p{s_i - \We_{\input(i)}\ndot\hidden\Wd_{\output(i)}}\We_{\input(i)}}_\text{``feature benefit''} - \UB{\sum_{j \ne i} \p{\We_{\input(j)}\ndot\hidden\Wd_{\output(i)}}\We_{\input(j)}}_\text{``interference''}.
}
\]
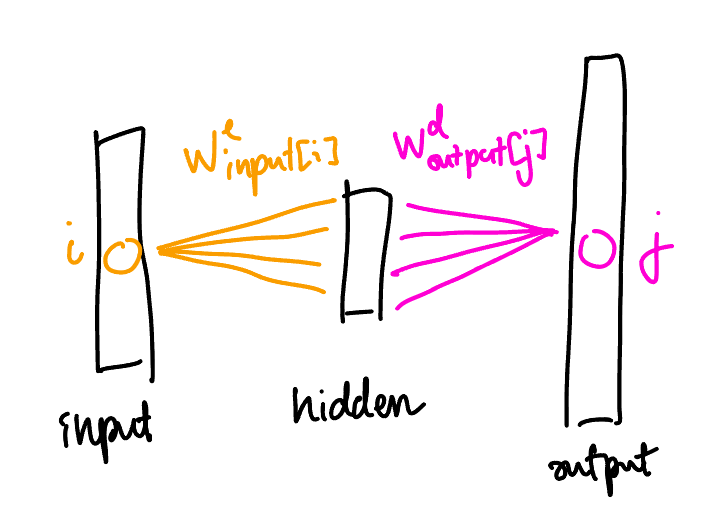
That is, there are two forces:
- feature benefit: the dot product between $\We_{\input(i)}$ and $\Wd_{\output(i)}$ is “trying” to be $s_i$ (they tend to align),
- interference: $\We_{\input(i)}$ and $\Wd_{\output(j)}$ are trying to be perpendicular when $i \ne j$ (they tend to repell each other).
This is very similar to the setup in Toy Models of Superposition, except that
- there are no ReLUs at the end,
- the encoding and decoding weights $\We$ and $\Wd$ are not tied together,
- the target values $s_i$ can be different from $1$.
Speed of learning
To simplify things, let’s assume that all $s_i$ are positive, $\We$ and $\Wd$ start out with
- $\We_{\input(i)}$ perpendicular to $\Wd_{\output(j)}$ when $i \ne j$,
- $\We_{\input(i)}=\Wd_{\output(i)}$.
Then interference disappears, and $\We_{\input(i)}$ will remain equal to $\Wd_{\output(i)}$ throughout training. Because of this, we’ll just refer to them both as $W_i$. Introducing a new variable $u_i \ce W_i\ndot\hidden W_i = \norm{W_i}_\hidden^2 \in \R$ to track their squared norm, we get
\[
\al{
\frac{\d u_i}{\d t}
&= 2\frac{\d W_i}{\d t}\ndot\hidden W_i\\
&= 2\b{\p{s_i - W_i\ndot\hidden W_i}W_i}\ndot\hidden W_i\\
&= 2\p{s_i - u_i}u_i.
}
\]
This is the differential equation of a logistic function: it solves to
\[
u_i(t) = \frac{s_i}{1+e^{-2s_i(t-t_0)}}.
\]
This means that $u_i$ takes time
- $\approx \log(s_i/\eps)/s_i$ to go from $\eps$ to $s_i/2$;
- $\approx \log(s_i/\eps)/s_i$ to go from $s_i/2$ to $s_i-\eps$.
In other words, the rate at which the values of the correlation matrix $\Sigma$ get learned is (roughly) proportional to those values!
Speed of lowering interference
This section is my own speculation.
Let’s keep the assumption that $\We_{\input(i)}=\Wd_{\output(i)}$ at the start (and therefore, throughout training), but relax the assumption that $W_i$ starts out perpendicular to $W_j$ when $i \ne j$. Then we can study at which rate the interference decreases.
It turns out that the right quantity to look at is the cosine similarity
\[
\eps_{ij} \ce \frac{W_i \ndot\hidden W_j}{\norm{W_i}_\hidden \norm{W_j}_\hidden}.
\]
Indeed, $\eps_{ij}$ doesn’t change when $W_i$ or $W_j$ gets scaled up by some factor (without changing direction), so the “feature benefit” part doesn’t affect $\eps_{ij}$: for the purposes of studying how fast $\eps_{ij}$ decreases at any point in time, the only relevant changes in $W_i$ are
\[
\frac{\d W_i}{\d t} = -\sum_{j \ne i}\p{W_i \ndot\hidden W_j}W_j.
\]
Then we have
\[
\al{
&\frac{\d \p{W_i \ndot\hidden W_j}}{\d t}\\
&\quad= \frac{\d W_i}{\d t}\ndot \hidden W_j + W_i \ndot\hidden \frac{\d W_j}{\d t}\\
&\quad= -\p{W_i \ndot \hidden W_j}\p{\norm{W_i}_\hidden^2 + \norm{W_j}_\hidden^2} - \UB{2\sum_{k \ne i,j}\p{W_i \ndot \hidden W_k}\p{W_j \ndot \hidden W_k}}_\text{second-order effects}
}
\]
Ignoring the second-order effects, we get
\[
\frac{\d \eps_{ij}}{\d t} \approx -\eps_{ij}\p{\norm{W_i}_\hidden^2 + \norm{W_j}_\hidden^2}.
\]
So $\eps_{ij}$ decreases exponentially at a rate proportional to the larger of the two squared norms $\norm{W_i}_\hidden^2$ and $\norm{W_j}_\hidden^2$. This means that the angle between $W_i$ and $W_j$ will start to approach $90\degree$ faster when one of $W_i$ or $W_j$ gets big. And that, as we’ve seen, depends on how big $s_i$ and $s_j$ are.
Summary of the dynamics
So we can summarize the dynamics of learning this way:
- the input-output correlations get learned one by one, in order of their goal value $s_i$;
- when $\We_{\input(i)}$ and $\Wd_{\output(i)}$ get learned, they quickly align and acquire the same length ($\We_{\input(i)} \approx \Wd_{\output(i)}$ if $s_i>0$ and $\We_{\input(i)} \approx -\Wd_{\output(i)}$ if $s_i < 0$);
- they eventually reach length $\sqrt{|s_i|}$;
- when $\We_{\input(i)}$/$\Wd_{\output(i)}$ get learned, they simultaneously repel all the other vectors into their perpendicular space.
Non-diagonal case
The striking thing with fully linear networks is that they’re completely rotationally invariant. For us, this means that even if $\Sigma$ is not diagonal, things will still happen the exact same way, but over the singular value decomposition of $\Sigma$ instead.
Suppose that $|\input| = |\output|\ec d$. Let’s rewrite $S$ as a sum of some singular modes (some of which might be $0$ if $\Sigma$ is not full-rank):
\[
\ndef{\inmode}{inmode}
\ndef{\outmode}{outmode}
\Sigma = \sum_{i=1}^D s_i(U_{\inmode(i)} \odot V_{\outmode(i)}) = U \ndot\inmode S \ndot\outmode V
\]
where $U \in \R^{\inmode\times\input}$, $V \in \R^{\outmode \times \output}$ are orthonormal bases of $\R^{\input}$ and $\R^{\output}$, and $S \in \R^{\inmode \times \outmode}$ is diagonal with values $s_1, \ldots, s_n$. Let’s also represent $\We$ and $\Wd$ under the new bases:
\[
\We = U \ndot\inmode\ol\We \qquad \Wd = \ol\Wd \ndot\outmode V.
\]
Then we have
\[
\al{
\partial \CL
&= 2\p{\Sigma - \We \ndot\hidden \Wd}\ndot{\input\\\output}\p{\partial\We \ndot\hidden \Wd + \We \ndot\hidden \partial \Wd}\\
&= 2\b{U \ndot{\inmode}\p{S - \ol\We \ndot\hidden \ol\Wd}\ndot\outmode V}\\
&\qquad\ndot{\input\\\output}\b{U \ndot\inmode \p{\partial\ol\We \ndot\hidden \ol\Wd + \ol\We \ndot\hidden \partial \ol\Wd} \ndot\outmode V}\\
&=2\p{S - \ol\We \ndot\hidden \ol\Wd}\ndot{\inmode\\\outmode}\p{\partial\ol\We \ndot\hidden \ol\Wd + \ol\We \ndot\hidden \partial \ol\Wd},
}
\]
(where the last equality is by orthonormality of $U,V$) so the new learning dynamics are
\[
\al{
\frac{\d\ol\We}{\d t} = -\frac{\partial\CL}{\partial\ol\We} &= 2\p{S - \We\ndot\hidden\Wd}\ndot\outmode\ol\Wd\\
\frac{\d\ol\Wd}{\d t} = -\frac{\partial\CL}{\partial\ol\Wd} &= 2\p{S - \ol\We\ndot\hidden\ol\Wd}\ndot\inmode\ol\We.
}
\]
This is exactly the same as what we had earlier, except that $\Sigma, \We, \Wd$ changed to $S, \ol\We,\ol\Wd$ respectively, and $S$ is guaranteed to be diagonal. That is, by performing a simple change of basis, we’ve completely reduced to the diagonal case over a new “virtual” linear neural network.
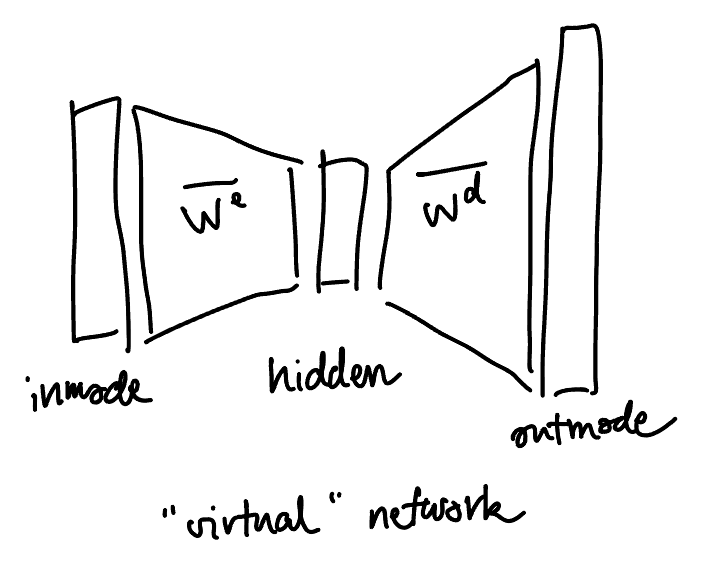
Also note that by rotational symmetry, if the initializations of $\We$ and $\Wd$ are i.i.d. Gaussians, then so are the initializations of $\ol\We$ and $\ol\Wd$.