$\require{mathtools}
%
%%% GENERIC MATH %%%
%
% Environments
\newcommand{\al}[1]{\begin{align}#1\end{align}} % need this for \tag{} to work
\renewcommand{\r}{\mathrm}
%
% Greek
\newcommand{\eps}{\epsilon}
\newcommand{\veps}{\varepsilon}
\let\fi\phi % because it looks like an f
\let\phi\varphi % because it looks like a p
%
% Miscellaneous shortcuts
% .. over and under
\newcommand{\ss}[1]{_{\substack{#1}}}
\newcommand{\ob}{\overbrace}
\newcommand{\ub}{\underbrace}
\newcommand{\ol}{\overline}
\newcommand{\tld}{\widetilde}
\newcommand{\HAT}{\widehat}
\newcommand{\f}{\frac}
\newcommand{\s}[2]{#1 /\mathopen{}#2}
\newcommand{\rt}{\sqrt}
% .. relations
\newcommand{\sr}{\stackrel}
\newcommand{\sse}{\subseteq}
\newcommand{\ce}{\coloneqq}
\newcommand{\ec}{\eqqcolon}
\newcommand{\ap}{\approx}
\newcommand{\ls}{\lesssim}
\newcommand{\gs}{\greatersim}
% .. miscer
\newcommand{\q}{\quad}
\newcommand{\qq}{\qquad}
\newcommand{\heart}{\heartsuit}
%
% Delimiters
% (I needed to create my own because the MathJax version of \DeclarePairedDelimiter doesn't have \mathopen{} and that messes up the spacing)
% .. one-part
\newcommand{\p}[1]{\mathopen{}\left( #1 \right)}
\newcommand{\b}[1]{\mathopen{}\left[ #1 \right]}
\newcommand{\set}[1]{\mathopen{}\left\{ #1 \right\}}
\newcommand{\abs}[1]{\mathopen{}\left\lvert #1 \right\rvert}
\newcommand{\floor}[1]{\mathopen{}\left\lfloor #1 \right\rfloor}
\newcommand{\ceil}[1]{\mathopen{}\left\lceil #1 \right\rceil}
\newcommand{\inner}[1]{\mathopen{}\left\langle #1 \right\rangle}
% .... (use phantom to force at least the standard height of double bars)
\newcommand{\norm}[1]{\mathopen{}\left\lVert #1 \vphantom{f} \right\rVert}
\newcommand{\frob}[1]{\norm{#1}_\mathrm{F}}
%% .. two-part
\newcommand{\incond}[2]{#1 \mathop{}\middle|\mathop{} #2}
\newcommand{\cond}[2]{ {\left.\incond{#1}{#2}\right.}}
\newcommand{\pco}[2]{\p{\incond{#1}{#2}}}
\newcommand{\bco}[2]{\b{\incond{#1}{#2}}}
\newcommand{\setco}[2]{\set{\incond{#1}{#2}}}
\newcommand{\at}[2]{\left.#1\right|_{#2}}
% ..... (use phantom to force at least the standard height of double bar)
\newcommand{\oldpara}[2]{#1\vphantom{f} \mathop{}\middle\|\mathop{} #2}
%\newcommand{\para}[2]{#1\vphantom{f} \mathop{}\middle\|\mathop{} #2}
\newcommand{\para}[2]{\mathchoice{\begin{matrix}#1\\\hdashline#2\end{matrix}}{\begin{smallmatrix}#1\\\hdashline#2\end{smallmatrix}}{\begin{smallmatrix}#1\\\hdashline#2\end{smallmatrix}}{\begin{smallmatrix}#1\\\hdashline#2\end{smallmatrix}}}
\newcommand{\ppa}[2]{\p{\para{#1}{#2}}}
\newcommand{\bpa}[2]{\b{\para{#1}{#2}}}
%\newcommand{\bpaco}[4]{\bpa{\incond{#1}{#2}}{\incond{#3}{#4}}}
\newcommand{\bpaco}[4]{\bpa{\cond{#1}{#2}}{\cond{#3}{#4}}}
%
% Levels of closeness
\newcommand{\scirc}[1]{\sr{\circ}{#1}}
\newcommand{\sdot}[1]{\sr{.}{#1}}
\newcommand{\slog}[1]{\sr{\log}{#1}}
\newcommand{\createClosenessLevels}[7]{
\newcommand{#2}{\mathrel{(#1)}}
\newcommand{#3}{\mathrel{#1}}
\newcommand{#4}{\mathrel{#1\!\!#1}}
\newcommand{#5}{\mathrel{#1\!\!#1\!\!#1}}
\newcommand{#6}{\mathrel{(\sdot{#1})}}
\newcommand{#7}{\mathrel{(\slog{#1})}}
}
\let\lt\undefined
\let\gt\undefined
% .. vanilla versions (is it within a constant?)
\newcommand{\ez}{\scirc=}
\newcommand{\eq}{\simeq}
\newcommand{\eqq}{\mathrel{\eq\!\!\eq}}
\newcommand{\eqqq}{\mathrel{\eq\!\!\eq\!\!\eq}}
\newcommand{\lez}{\scirc\le}
\newcommand{\lq}{\preceq}
\newcommand{\lqq}{\mathrel{\lq\!\!\lq}}
\newcommand{\lqqq}{\mathrel{\lq\!\!\lq\!\!\lq}}
\newcommand{\gez}{\scirc\ge}
\newcommand{\gq}{\succeq}
\newcommand{\gqq}{\mathrel{\gq\!\!\gq}}
\newcommand{\gqqq}{\mathrel{\gq\!\!\gq\!\!\gq}}
\newcommand{\lz}{\scirc<}
\newcommand{\lt}{\prec}
\newcommand{\ltt}{\mathrel{\lt\!\!\lt}}
\newcommand{\lttt}{\mathrel{\lt\!\!\lt\!\!\lt}}
\newcommand{\gz}{\scirc>}
\newcommand{\gt}{\succ}
\newcommand{\gtt}{\mathrel{\gt\!\!\gt}}
\newcommand{\gttt}{\mathrel{\gt\!\!\gt\!\!\gt}}
% .. dotted versions (is it equal in the limit?)
\newcommand{\ed}{\sdot=}
\newcommand{\eqd}{\sdot\eq}
\newcommand{\eqqd}{\sdot\eqq}
\newcommand{\eqqqd}{\sdot\eqqq}
\newcommand{\led}{\sdot\le}
\newcommand{\lqd}{\sdot\lq}
\newcommand{\lqqd}{\sdot\lqq}
\newcommand{\lqqqd}{\sdot\lqqq}
\newcommand{\ged}{\sdot\ge}
\newcommand{\gqd}{\sdot\gq}
\newcommand{\gqqd}{\sdot\gqq}
\newcommand{\gqqqd}{\sdot\gqqq}
\newcommand{\ld}{\sdot<}
\newcommand{\ltd}{\sdot\lt}
\newcommand{\lttd}{\sdot\ltt}
\newcommand{\ltttd}{\sdot\lttt}
\newcommand{\gd}{\sdot>}
\newcommand{\gtd}{\sdot\gt}
\newcommand{\gttd}{\sdot\gtt}
\newcommand{\gtttd}{\sdot\gttt}
% .. log versions (is it equal up to log?)
\newcommand{\elog}{\slog=}
\newcommand{\eqlog}{\slog\eq}
\newcommand{\eqqlog}{\slog\eqq}
\newcommand{\eqqqlog}{\slog\eqqq}
\newcommand{\lelog}{\slog\le}
\newcommand{\lqlog}{\slog\lq}
\newcommand{\lqqlog}{\slog\lqq}
\newcommand{\lqqqlog}{\slog\lqqq}
\newcommand{\gelog}{\slog\ge}
\newcommand{\gqlog}{\slog\gq}
\newcommand{\gqqlog}{\slog\gqq}
\newcommand{\gqqqlog}{\slog\gqqq}
\newcommand{\llog}{\slog<}
\newcommand{\ltlog}{\slog\lt}
\newcommand{\lttlog}{\slog\ltt}
\newcommand{\ltttlog}{\slog\lttt}
\newcommand{\glog}{\slog>}
\newcommand{\gtlog}{\slog\gt}
\newcommand{\gttlog}{\slog\gtt}
\newcommand{\gtttlog}{\slog\gttt}
%
% Miscellaneous
\newcommand{\LHS}{\mathrm{LHS}}
\newcommand{\RHS}{\mathrm{RHS}}
% .. operators
\DeclareMathOperator{\poly}{poly}
\DeclareMathOperator{\polylog}{polylog}
\DeclareMathOperator{\quasipoly}{quasipoly}
\DeclareMathOperator{\negl}{negl}
\DeclareMathOperator*{\argmin}{arg\,min}
\DeclareMathOperator*{\argmax}{arg\,max}
% .. functions
\DeclareMathOperator{\id}{id}
\DeclareMathOperator{\sign}{sign}
\DeclareMathOperator{\err}{err}
\DeclareMathOperator{\ReLU}{ReLU}
% .. analysis
\let\d\undefined
\newcommand{\d}{\operatorname{d}\mathopen{}}
\newcommand{\df}[2]{\f{\d #1}{\d #2}}
\newcommand{\ds}[2]{\s{\d #1}{\d #2}}
\newcommand{\part}{\partial}
\newcommand{\partf}[2]{\f{\part #1}{\part #2}}
\newcommand{\parts}[2]{\s{\part #1}{\part #2}}
\newcommand{\grad}[1]{\mathop{\nabla\!_{#1}}}
% .. sets
\newcommand{\N}{\mathbb{N}}
\newcommand{\Z}{\mathbb{Z}}
\newcommand{\R}{\mathbb{R}}
\newcommand{\C}{\mathbb{C}}
\newcommand{\F}{\mathbb{F}}
\newcommand{\zo}{\set{0,1}}
\newcommand{\pmo}{\set{\pm 1}}
%
%%% SPECIALIZED MATH %%%
%
% Logic
\renewcommand{\and}{\wedge}
\newcommand{\AND}{\bigwedge}
\newcommand{\or}{\vee}
\newcommand{\OR}{\bigvee}
\newcommand{\xor}{\oplus}
\newcommand{\XOR}{\bigoplus}
\newcommand{\union}{\cup}
\newcommand{\inter}{\cap}
\newcommand{\UNION}{\bigcup}
\newcommand{\INTER}{\bigcap}
\newcommand{\comp}{\overline}
\newcommand{\true}{\r{true}}
\newcommand{\false}{\r{false}}
\newcommand{\tf}{\set{\true,\false}}
\DeclareMathOperator{\One}{\mathbb{1}}
\DeclareMathOperator{\1}{\mathbb{1}}
%
% Linear algebra
\renewcommand{\span}{\mathrm{span}}
\DeclareMathOperator{\rank}{rank}
\DeclareMathOperator{\proj}{proj}
\DeclareMathOperator{\dom}{dom}
\DeclareMathOperator{\Img}{Im}
\newcommand{\transp}{\mathsf{T}}
\renewcommand{\t}{^\transp}
% ... named tensors
\newcommand{\namedtensorstrut}{\vphantom{fg}} % milder than \mathstrut
\newcommand{\name}[1]{\mathsf{\namedtensorstrut #1}}
\newcommand{\nbin}[2]{\mathbin{\underset{\substack{#1}}{\namedtensorstrut #2}}}
\newcommand{\ndot}[1]{\nbin{#1}{\odot}}
\newcommand{\ncat}[1]{\nbin{#1}{\oplus}}
\newcommand{\nsum}[1]{\sum\limits_{\substack{#1}}}
\newcommand{\nfun}[2]{\mathop{\underset{\substack{#1}}{\namedtensorstrut\mathrm{#2}}}}
\newcommand{\ndef}[2]{\newcommand{#1}{\name{#2}}}
\newcommand{\nt}[1]{^{\transp(#1)}}
%
% Probability
\newcommand{\Normal}{\mathcal{N}}
\let\Pr\undefined
\DeclareMathOperator*{\Pr}{Pr}
\DeclareMathOperator*{\G}{\mathbb{G}}
\DeclareMathOperator*{\Odds}{Od}
\DeclareMathOperator*{\E}{E}
\DeclareMathOperator*{\Var}{Var}
\DeclareMathOperator*{\Cov}{Cov}
\DeclareMathOperator*{\corr}{corr}
\DeclareMathOperator*{\median}{median}
\newcommand{\dTV}{d_{\mathrm{TV}}}
\newcommand{\dHel}{d_{\mathrm{Hel}}}
\newcommand{\dJS}{d_{\mathrm{JS}}}
% ... information theory
\let\H\undefined
\DeclareMathOperator*{\H}{H}
\DeclareMathOperator*{\I}{I}
\DeclareMathOperator*{\D}{D}
%
%%% SPECIALIZED COMPUTER SCIENCE %%%
%
% Complexity classes
% .. classical
\newcommand{\Poly}{\mathsf{P}}
\newcommand{\NP}{\mathsf{NP}}
\newcommand{\PH}{\mathsf{PH}}
\newcommand{\PSPACE}{\mathsf{PSPACE}}
\renewcommand{\L}{\mathsf{L}}
% .. probabilistic
\newcommand{\formost}{\mathsf{Я}}
\newcommand{\RP}{\mathsf{RP}}
\newcommand{\BPP}{\mathsf{BPP}}
\newcommand{\MA}{\mathsf{MA}}
\newcommand{\AM}{\mathsf{AM}}
\newcommand{\IP}{\mathsf{IP}}
\newcommand{\RL}{\mathsf{RL}}
% .. circuits
\newcommand{\NC}{\mathsf{NC}}
\newcommand{\AC}{\mathsf{AC}}
\newcommand{\ACC}{\mathsf{ACC}}
\newcommand{\TC}{\mathsf{TC}}
\newcommand{\Ppoly}{\mathsf{P}/\poly}
\newcommand{\Lpoly}{\mathsf{L}/\poly}
% .. resources
\newcommand{\TIME}{\mathsf{TIME}}
\newcommand{\SPACE}{\mathsf{SPACE}}
\newcommand{\TISP}{\mathsf{TISP}}
\newcommand{\SIZE}{\mathsf{SIZE}}
% .. keywords
\newcommand{\co}{\mathsf{co}}
\newcommand{\Prom}{\mathsf{Promise}}
%
% Boolean analysis
\newcommand{\harpoon}{\!\upharpoonright\!}
\newcommand{\rr}[2]{#1\harpoon_{#2}}
\newcommand{\Fou}[1]{\widehat{#1}}
\DeclareMathOperator{\Ind}{\mathrm{Ind}}
\DeclareMathOperator{\Inf}{\mathrm{Inf}}
\DeclareMathOperator{\Der}{\mathrm{D}}
\DeclareMathOperator{\Stab}{\mathrm{Stab}}
\DeclareMathOperator{\T}{T}
\DeclareMathOperator{\sens}{\mathrm{s}}
\DeclareMathOperator{\bsens}{\mathrm{bs}}
\DeclareMathOperator{\fbsens}{\mathrm{fbs}}
\DeclareMathOperator{\Cert}{\mathrm{C}}
\DeclareMathOperator{\DT}{\mathrm{DT}}
\DeclareMathOperator{\CDT}{\mathrm{CDT}} % canonical
\DeclareMathOperator{\ECDT}{\mathrm{ECDT}}
\DeclareMathOperator{\CDTv}{\mathrm{CDT_{vars}}}
\DeclareMathOperator{\ECDTv}{\mathrm{ECDT_{vars}}}
\DeclareMathOperator{\CDTt}{\mathrm{CDT_{terms}}}
\DeclareMathOperator{\ECDTt}{\mathrm{ECDT_{terms}}}
\DeclareMathOperator{\CDTw}{\mathrm{CDT_{weighted}}}
\DeclareMathOperator{\ECDTw}{\mathrm{ECDT_{weighted}}}
\DeclareMathOperator{\AvgDT}{\mathrm{AvgDT}}
\DeclareMathOperator{\PDT}{\mathrm{PDT}} % partial decision tree
\DeclareMathOperator{\DTsize}{\mathrm{DT_{size}}}
\DeclareMathOperator{\W}{\mathbf{W}}
% .. functions (small caps sadly doesn't work)
\DeclareMathOperator{\Par}{\mathrm{Par}}
\DeclareMathOperator{\Maj}{\mathrm{Maj}}
\DeclareMathOperator{\HW}{\mathrm{HW}}
\DeclareMathOperator{\Th}{\mathrm{Th}}
\DeclareMathOperator{\Tribes}{\mathrm{Tribes}}
\DeclareMathOperator{\RotTribes}{\mathrm{RotTribes}}
\DeclareMathOperator{\CycleRun}{\mathrm{CycleRun}}
\DeclareMathOperator{\SAT}{\mathrm{SAT}}
\DeclareMathOperator{\UniqueSAT}{\mathrm{UniqueSAT}}
%
% Dynamic optimality
\newcommand{\OPT}{\mathsf{OPT}}
\newcommand{\Alt}{\mathsf{Alt}}
\newcommand{\Funnel}{\mathsf{Funnel}}
%
% Alignment
\DeclareMathOperator{\Amp}{\mathrm{Amp}}
%
%%% TYPESETTING %%%
%
% In text
\renewcommand{\th}{^{\mathrm{th}}}
\newcommand{\degree}{^\circ}
%
% Fonts
% .. bold
\newcommand{\BA}{\boldsymbol{A}}
\newcommand{\BB}{\boldsymbol{B}}
\newcommand{\BC}{\boldsymbol{C}}
\newcommand{\BD}{\boldsymbol{D}}
\newcommand{\BE}{\boldsymbol{E}}
\newcommand{\BF}{\boldsymbol{F}}
\newcommand{\BG}{\boldsymbol{G}}
\newcommand{\BH}{\boldsymbol{H}}
\newcommand{\BI}{\boldsymbol{I}}
\newcommand{\BJ}{\boldsymbol{J}}
\newcommand{\BK}{\boldsymbol{K}}
\newcommand{\BL}{\boldsymbol{L}}
\newcommand{\BM}{\boldsymbol{M}}
\newcommand{\BN}{\boldsymbol{N}}
\newcommand{\BO}{\boldsymbol{O}}
\newcommand{\BP}{\boldsymbol{P}}
\newcommand{\BQ}{\boldsymbol{Q}}
\newcommand{\BR}{\boldsymbol{R}}
\newcommand{\BS}{\boldsymbol{S}}
\newcommand{\BT}{\boldsymbol{T}}
\newcommand{\BU}{\boldsymbol{U}}
\newcommand{\BV}{\boldsymbol{V}}
\newcommand{\BW}{\boldsymbol{W}}
\newcommand{\BX}{\boldsymbol{X}}
\newcommand{\BY}{\boldsymbol{Y}}
\newcommand{\BZ}{\boldsymbol{Z}}
\newcommand{\Ba}{\boldsymbol{a}}
\newcommand{\Bb}{\boldsymbol{b}}
\newcommand{\Bc}{\boldsymbol{c}}
\newcommand{\Bd}{\boldsymbol{d}}
\newcommand{\Be}{\boldsymbol{e}}
\newcommand{\Bf}{\boldsymbol{f}}
\newcommand{\Bg}{\boldsymbol{g}}
\newcommand{\Bh}{\boldsymbol{h}}
\newcommand{\Bi}{\boldsymbol{i}}
\newcommand{\Bj}{\boldsymbol{j}}
\newcommand{\Bk}{\boldsymbol{k}}
\newcommand{\Bp}{\boldsymbol{p}}
\newcommand{\Bq}{\boldsymbol{q}}
\newcommand{\Br}{\boldsymbol{r}}
\newcommand{\Bs}{\boldsymbol{s}}
\newcommand{\Bt}{\boldsymbol{t}}
\newcommand{\Bu}{\boldsymbol{u}}
\newcommand{\Bv}{\boldsymbol{v}}
\newcommand{\Bw}{\boldsymbol{w}}
\newcommand{\Bx}{\boldsymbol{x}}
\newcommand{\By}{\boldsymbol{y}}
\newcommand{\Bz}{\boldsymbol{z}}
\newcommand{\Balpha}{\boldsymbol{\alpha}}
\newcommand{\Bbeta}{\boldsymbol{\beta}}
\newcommand{\Bgamma}{\boldsymbol{\gamma}}
\newcommand{\Bdelta}{\boldsymbol{\delta}}
\newcommand{\Beps}{\boldsymbol{\eps}}
\newcommand{\Bveps}{\boldsymbol{\veps}}
\newcommand{\Bzeta}{\boldsymbol{\zeta}}
\newcommand{\Beta}{\boldsymbol{\eta}}
\newcommand{\Btheta}{\boldsymbol{\theta}}
\newcommand{\Biota}{\boldsymbol{\iota}}
\newcommand{\Bkappa}{\boldsymbol{\kappa}}
\newcommand{\Blambda}{\boldsymbol{\lambda}}
\newcommand{\Bmu}{\boldsymbol{\mu}}
\newcommand{\Bnu}{\boldsymbol{\nu}}
\newcommand{\Bxi}{\boldsymbol{\xi}}
\newcommand{\Bomicron}{\boldsymbol{\omicron}}
\newcommand{\Bpi}{\boldsymbol{\pi}}
\newcommand{\Brho}{\boldsymbol{\rho}}
\newcommand{\Bsigma}{\boldsymbol{\sigma}}
\newcommand{\Btau}{\boldsymbol{\tau}}
\newcommand{\Bupsilon}{\boldsymbol{\upsilon}}
\newcommand{\Bphi}{\boldsymbol{\phi}}
\newcommand{\Bfi}{\boldsymbol{\fi}}
\newcommand{\Bchi}{\boldsymbol{\chi}}
\newcommand{\Bpsi}{\boldsymbol{\psi}}
\newcommand{\Bomega}{\boldsymbol{\omega}}
% .. calligraphic
\newcommand{\CA}{\mathcal{A}}
\newcommand{\CB}{\mathcal{B}}
\newcommand{\CC}{\mathcal{C}}
\newcommand{\CD}{\mathcal{D}}
\newcommand{\CE}{\mathcal{E}}
\newcommand{\CF}{\mathcal{F}}
\newcommand{\CG}{\mathcal{G}}
\newcommand{\CH}{\mathcal{H}}
\newcommand{\CI}{\mathcal{I}}
\newcommand{\CJ}{\mathcal{J}}
\newcommand{\CK}{\mathcal{K}}
\newcommand{\CL}{\mathcal{L}}
\newcommand{\CM}{\mathcal{M}}
\newcommand{\CN}{\mathcal{N}}
\newcommand{\CO}{\mathcal{O}}
\newcommand{\CP}{\mathcal{P}}
\newcommand{\CQ}{\mathcal{Q}}
\newcommand{\CR}{\mathcal{R}}
\newcommand{\CS}{\mathcal{S}}
\newcommand{\CT}{\mathcal{T}}
\newcommand{\CU}{\mathcal{U}}
\newcommand{\CV}{\mathcal{V}}
\newcommand{\CW}{\mathcal{W}}
\newcommand{\CX}{\mathcal{X}}
\newcommand{\CY}{\mathcal{Y}}
\newcommand{\CZ}{\mathcal{Z}}
% .. typewriter
\newcommand{\TA}{\mathtt{A}}
\newcommand{\TB}{\mathtt{B}}
\newcommand{\TC}{\mathtt{C}}
\newcommand{\TD}{\mathtt{D}}
\newcommand{\TE}{\mathtt{E}}
\newcommand{\TF}{\mathtt{F}}
\newcommand{\TG}{\mathtt{G}}
\newcommand{\TH}{\mathtt{H}}
\newcommand{\TI}{\mathtt{I}}
\newcommand{\TJ}{\mathtt{J}}
\newcommand{\TK}{\mathtt{K}}
\newcommand{\TL}{\mathtt{L}}
\newcommand{\TM}{\mathtt{M}}
\newcommand{\TN}{\mathtt{N}}
\newcommand{\TO}{\mathtt{O}}
\newcommand{\TP}{\mathtt{P}}
\newcommand{\TQ}{\mathtt{Q}}
\newcommand{\TR}{\mathtt{R}}
\newcommand{\TS}{\mathtt{S}}
\newcommand{\TT}{\mathtt{T}}
\newcommand{\TU}{\mathtt{U}}
\newcommand{\TV}{\mathtt{V}}
\newcommand{\TW}{\mathtt{W}}
\newcommand{\TX}{\mathtt{X}}
\newcommand{\TY}{\mathtt{Y}}
\newcommand{\TZ}{\mathtt{Z}}$
Adapted from sections 1.7 and 1.8 of “Boolean function complexity” by Stasys Jukna.
It’s kind of hard to prove lower bounds for functions. On the other hand, mathematicians seem to have a pretty good grasp on graphs, so maybe we could get hardness from graphs and import it to functions?
For any function $f : \zo^n \to \zo$, you can associate with it a huge bipartite graph $G_f$ where both halves have $N \ce 2^{n/2}$ vertices: for any two strings $u, v \in \zo^{n/2}$, create an edge between $u$ and $v$ iff <div>[f(u_1, \ldots, u_{n/2}, v_1, \ldots, v_{n/2}) = 1.]</div>
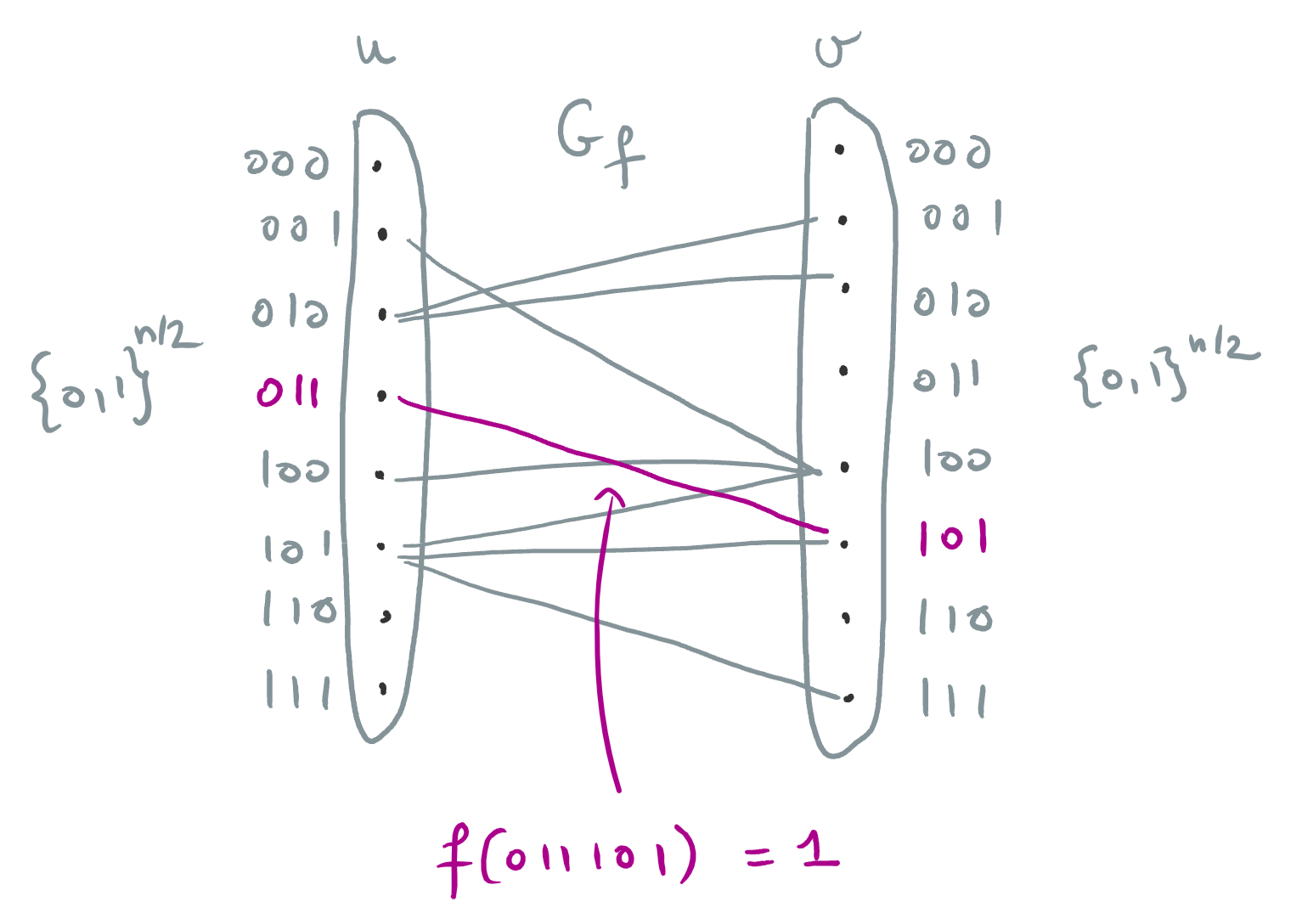
The main cool thing about this transformation is that the graph $G_f$ is huge. This means that if we can establish links between the computation costs of $f$ and $G_f$ (and we will), then relatively modest lower bounds for $G_f$ give huge lower bounds for $f$: the bounds magnify. For example, a lower bound of $N^\eps$ for $G_f$ gives a lower bound of $(2^{n/2})^\eps = 2^{\Omega(n)}$ for $f$, and a lower bound of $(\log N)^c$ for $G_f$ gives a lower bound of $(\log (2^{n/2}))^c = \Omega(n^c)$ for $f$.
Clique complexity
Imagine we have some small formula computing $f$, made of fanin-2 $\and,\or$ gates, and literals $x_i, \comp{x_i}$ at the leaves. What does this mean for $G_f$?
- The $\and,\or$ gates correspond to intersection and union of graphs respectively. For example, if $f = g \and h$, then $G_f$ is the graph where $(u,v)$ is an edge iff $(u,v)$ is an edge in both $G_g$ and $G_h$.
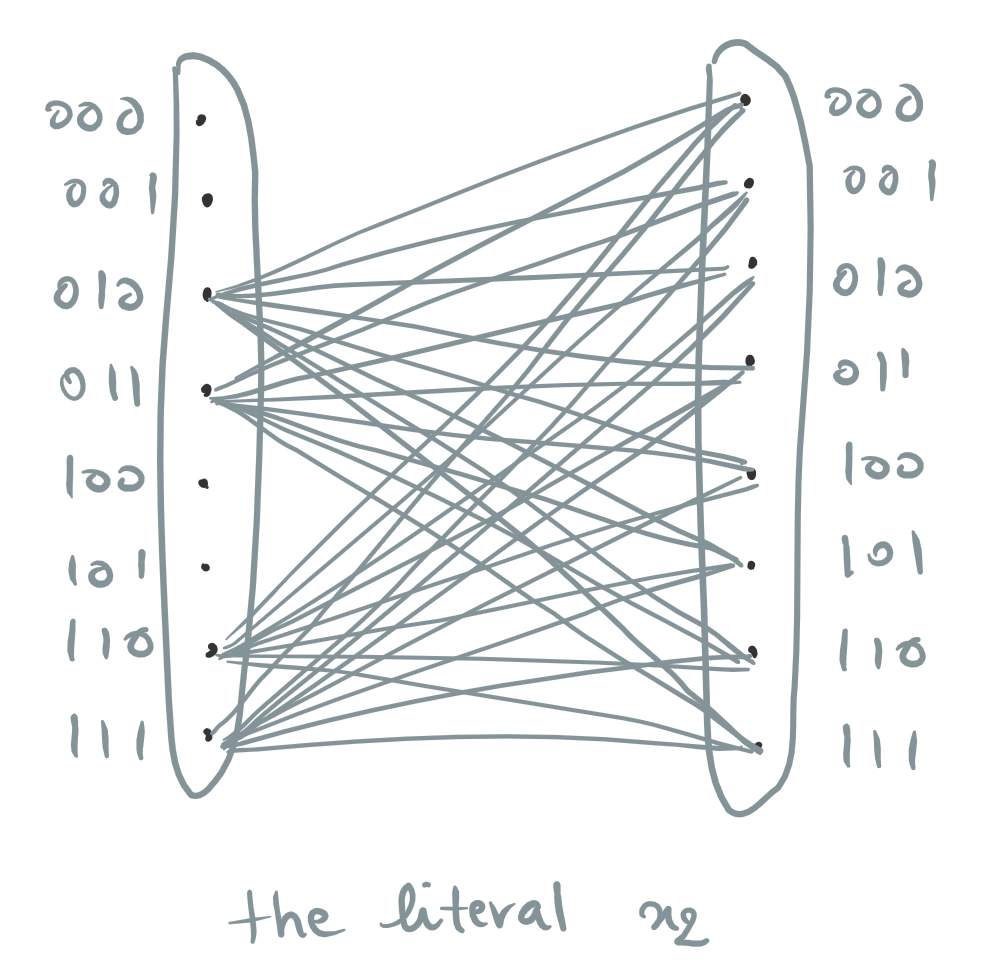
- The literal $x_i$ corresponds to the graph made of every edge $(u,v)$ where $u_i = 1$ (if $i\le n/2$), or where $v_{i-n/2} = 1$ (if $i > n/2$). The literal $\comp{x_i}$ is the same but with $0$ instead of $1$. In either case, this is a (bipartite) clique: the set of edges is of the form $S \times T$ for some subsets of vertices $S, T \sse \zo^{n/2} = [N]$.
This suggests defining the (formula) clique complexity of a graph $G$: the size of the smallest formula computing $G$, made of fanin-2 $\inter, \union$ gates, and arbitrary bipartite cliques at the leaves. Note that the clique complexity of $G_f$ might be much smaller than the formula size of $f$, since we’re allowing arbitrary bipartite cliques $S \times T$ at the leaves (of which there are $(2^{N})^2 = 2^{2^{\Theta(n)}}$), not just the specific $2n$ cliques that arise from literals $x_i, \comp{x_i}$. But the clique complexity of $G_f$ is clearly a lower bound on the formula size of $f$.
The clique complexity can range from $1$ to $\Theta(N)$:
- Any bipartite clique (including the complete graph) trivially has clique complexity $1$.
- Any graph can be represented as the union of $\le N$ cliques of the form $\set{u} \times T$.
- Most graphs have clique complexity $\Omega(N)$ by the following counting argument. There are only $(2^N)^2 = 2^{2N}$ possible cliques, so there are only $2^{O(t)}\cdot (2^{2N})^t$ possible formulas with $t$ leaves. On the other hand, there are $2^{N^2}$ graphs total, so we must have $t \geq \Omega(N)$ for most.
The best formula size lower bound we know for an explicit function is $\Omega(n^3)$. So to improve the state of the art, it would be enough to prove a $\omega((\log N)^3)$ lower bound on clique complexity. On the other hand, proving such lower bounds might be quite hard. For example, the parity function requires formulas of size $\Omega(n^2) = \Omega((\log N)^2)$, but as a graph, its clique complexity is $2$: it’s the union of two bipartite cliques, one joining strings of even parity on the left to strings of odd parity on the right
\[\set{u \in \zo^{n/2} \mid u_1 \xor \cdots \xor u_{n/2} = 0} \times \set{v \in \zo^{n/2} \mid v_1 \xor \cdots \xor v_{n/2} = 1},\]
and one with the roles swapped
\[\set{u \in \zo^{n/2} \mid u_1 \xor \cdots \xor u_{n/2} = 1} \times \set{v \in \zo^{n/2} \mid v_1 \xor \cdots \xor v_{n/2} = 0}.\]
Note: Here, we looked at formula size, but as far as I can tell, we could equally well have looked at circuit size and adapted the definition of clique complexity accordingly. In that case, $\omega(\log N)$ would be enough to beat the state of the art.
Star complexity
Another way to define graph complexity is to let stars (instead of cliques) be the basic building blocks: we’ll start from graphs of the form $\set{u} \times [N]$ and $[N] \times \set{v}$.
Unbounded fan-in
This works particularly well when the model we consider on top of that allows unions of unbounded fanin at the bottom: then we can form the graph corresponding to any literal $x_i, \comp{x_i}$ with just one $\union$ gate. For example, for the literal $x_i$ with $i \leq n/2$, we take the union of the $2^{n/2}/2$ stars $\set{u} \times \zo^{n/2}$ with $u_i = 1$.
This means that whenever we have some circuit for $f$, we can turn it into a circuit for $G_f$ by:
- turning all the $\and,\or$ into $\inter,\union$;
- replacing each occurrence of the literals $x_i, \comp{x_i}$ by one of $2n$ additional $\union$ gates
with fanin $2^{n/2}/2$ (corresponding to the above construction).
This circuit only has $2n$ more gates than $f$ does, so if we get a strong enough lower bound on the size needed to compute $G_f$ (say $\omega(\log N) = \omega(n)$), we get the same lower bound for $f$. And in fact, if the circuit model we’re considering for $f$ already has unbounded-fanin OR gates at the bottom, then those $2n$ additional $\union$ gates can be merged the bottom $\union$ gates from $f$, with no increase in depth or size ar size at all.
So for example, if we wanted to prove lower bounds against depth-3 $\AC^0$ circuits, we could define the “$\Sigma_3$ star complexity” of a graph $G$: the smallest size (in number of gates) of a $\union$-$\inter$-$\union$ circuit computing $G$, with unbounded fanin and stars at the leaves.
Similarly to clique complexity, the $\Sigma_3$ star complexity ranges between $1$ and $\Theta(N)$.
- Any graph of the form $S \times [N]$ or $[N] \times T$ can be represented with just one $\union$ gate.
- We can form any partial star $\set{u} \times T$ with two gates (it’s the intersection of the star $\set{u} \times [N]$ with the graph $[N] \times T$ as above), and any graph can be represented as the union of $\le N$ such partial stars, so the total size is $\le 2N+1$.
- Most graphs require size $\Omega(N)$ by the following counting argument. There are $2N$ stars, so in a circuit of size $t$, each gate multiplies the possibilities by $O(2^{2N+t})$ based on what stars and gates it connects to. Thus there are $O(2^{2N+t})^t$ circuits of size $t$. On the other hand, there are $2^{N^2}$ graphs, so we need $t \geq \Omega(N)$ for most of them.
Any lower bound of the form $N^\eps$ on the $\Sigma_3$ star complexity of $G_f$ would give a truly exponential $(2^{n/2})^\eps = 2^{\Omega(n)}$ lower bound on the size of $\Sigma_3$ circuits for $f$. For now, the best known lower bound is $2^{\Theta(\sqrt{n})}$, so this would be an incredible breakthrough. In particular, by Valiant’s depth reduction, this would imply super-linear lower bounds for $\NC^1$.
But as with clique complexity, lower bounds might be very hard to obtain. Taking the parity function as an example again, it requires depth-$3$ circuits of size $2^{\Omega(\sqrt{n})}$, but as a graph, its $\Sigma_3$ star complexity is $\leq 7$: indeed,
\[\Par_n(u,v) = 1 \Leftrightarrow \p{\XOR_i u_i = 0 \and \XOR_i v_i = 1} \or \p{\XOR_i u_i = 1 \and \XOR_i v_i = 0},\]
and each internal statement such as “$\XOR_i u_i = 0$” can be expressed as a union of stars.
Bounded fan-in
In fact, even without unbounded-fanin $\union$ gates, forming the graphs that correspond to the literals $x_i, \comp{x_i}$ isn’t that expensive. We can do construct each of them trivially using $\leq 2^{n/2} = N$ union gates, for a total of $O(nN) = O(N \log N)$ size. So maybe even “regular old” circuit size would do?
Let’s define the (fanin-2 circuit) star complexity of a graph $G$ as the size of the smallest circuit computing $G$, made of fanin-2 $\inter,\union$ gates and with stars at the bottom. Then the star complexity of $G_f$ is at most $O(N \log N)$ plus the (fanin-2) circuit size of $f$.
The star complexity mostly ranges between $\Theta(N)$ and $\Theta(N^2/\log N)$:
- Each star contains only $N$ edges, so any graph that’s dense (i.e. has $\Omega(N^2)$ edges) needs at least $\Omega(N)$ stars to be described.
- Any graph can be represented with size $O(N^2)$: you can form any partial star $\set{u} \times T$ using $O(N)$ gates, then union them together. To get $O(N^2 / \log N)$, we can apply Lupanov’s construction that gives a circuit of size $O(2^n/n) = O(N^2 / \log N)$ for any function $f$, then apply the transformation to a star circuit.
- Most graphs require size $\Omega(N^2 / \log N)$ by the following counting argument. In a circuit of size $t$, you can describe any gate by saying its type and which two stars or gates it has as inputs, which gives $2\cdot (2N+t)^2$ possibilities. So overall, there are at most $(N+t)^{O(t)}$ circuits, while there are $2^{N^2}$ graphs, so there most need $t \geq \Omega(N^2 / \log N)$.
So this $O(N \log N)$ additive term that we needed to express the literals $x_i, \comp{x_i}$ is not necessarily an issue: as long as you get a lower that’s bigger than $\omega(N \log N)$ on the complexity of $G_f$, that gives you a truly exponential $\omega(N \log N) = \omega(2^{n/2} \cdot (n/2)) = 2^{\Omega(n)}$ bound on the circuit size of $f$.
Reducing the overhead to $O(N)$
But in fact, we can even get that $O(N \log N)$ term down to $O(N)$ by reusing some intermediate computations while forming the literals $x_i, \comp{x_i}$. Let’s show how you can do this for $i \le n/2$ (i.e. literals on the “left side”); the other case is similar.
First, we’ll form unions of all stars $\set{u} \times [N]$ for strings $u$ that share some prefix: for each length $0 \le l \le n/2$ and each string $p \in \zo^l$, we’ll form the “prefix union” $\set{u \in \zo^{n/2} \mid u_{[l]} = p} \times [N]$. There are $\sum_{l=0}^{n/2} 2^l = O(N)$ such prefix unions, and can form them all using $O(N)$ union gates:
- when $l=n/2$, it’s just the stars $\set{p} \times [N]$ themselves;
- when $l<n/2$, you can build each one from two prefix unions with length $l+1$, since
\[\set{u \mid u_{[l]} = p} = \set{u \mid u_{[l+1]} = p0} \union \set{u \mid u_{[l+1]} = p1}.\]
Then, for any $i \in [n/2]$ and bit $b \in \zo$, you can form the union $\set{u \mid u_i = b} \times [N]$ by taking the union of the $2^{i-1}$ prefix unions with length $l=i$ for which $p$ ends in $b$. These correspond to the literals $x_i$ and $\comp{x_i}$. This again only takes $O(N)$ gates.
This means that actually, the star complexity of $G_f$ is at most $O(N)$ plus the circuit size of $f$! More precisely, the overhead is $\leq 6N$ if you count carefully, which means that a lower bound of just $7N$ on $G_f$’s star complexity would give exponential lower bounds on $f$’s circuit size. Since lower bounds of the form $\Omega(N)$ are trivial (just pick a dense graph), if you want to be cheeky, you could say that we’re “only a constant factor away from proving $\Poly \ne \NP$”.