$$

Adapted from lectures 10 and 11 of Ryan O’Donnell’s Fall 2017 graduate complexity theory class at CMU.

In Buying randomness with quantifiers, we saw that in some cases, we can trade randomness for $\mathrm{\forall }$ or $\mathrm{\exists }$ quantifiers, proving that $\mathsf{BPP}$ is in $\mathsf{P}/\mathrm{poly}$ and ${\mathrm{\Sigma }}_2\mathsf{P}$. In this note, we extract the essence of those two proofs and apply the tricks more generally, with a focus on Arthur-Merlin complexity classes.

An interlude on quantifier notation

Since both of the two tricks we’ve seen allowed us to “play with the quantifiers” in the definitions of complexity classes in specific ways, it would be useful to make this more systematic by encapsulating the definitions of many complexity classes using quantifiers only.

For example, ${\mathrm{\Sigma }}_2\mathsf{P}$ corresponds to the languages $L$ for which there is a verifier $V$ such that¹

• if $x\in L$, then $\mathrm{\exists }y,\mathrm{\forall }z:V(x,y,z)=1$;
• if $x\notin L$, then $\mathrm{\forall }y,\mathrm{\exists }z:V(x,y,z)=0$.

Because the quantifiers are $\mathrm{\exists }\mathrm{\forall }$ in one case and $\mathrm{\forall }\mathrm{\exists }$ in the other, we will simply call this class “$\mathrm{\exists }\mathrm{\forall }/\mathrm{\forall }\mathrm{\exists }$”. In general, by “$Q_1,\dots Q_k/Q_1^{\prime },\dots ,Q_k^{\prime }$” (where $Q_i,Q_i^{\prime }$ are quantifiers in $\mathrm{\exists },\mathrm{\forall },\mathsf{Я}$), we mean the class of all languages $L$ for which there is a verifier $V$ such that

• if $x\in L$, then $Q_1{y}_1,\dots ,Q_k{y}_k:V(x,y_1,\dots ,y_k)=1$;
• if $x\notin L$, then $Q_1^{\prime }{y}_y,\dots ,Q_k^{\prime }{y}_k:V(x,y_1,\dots ,y_k)=0$.

As such, the reader is encourage to verify that $\mathsf{P}=/$, $\mathsf{NP}=\mathrm{\exists }/\mathrm{\forall }$, $\mathsf{co}\mathsf{NP}=\mathrm{\forall }/\mathrm{\exists }$, ${\mathrm{\Pi }}_2\mathsf{P}=\mathrm{\forall }\mathrm{\exists }/\mathrm{\exists }\mathrm{\forall }$, $\mathsf{BPP}=\mathsf{Я}/\mathsf{Я}$, $\mathsf{RP}=\mathsf{Я}/\mathrm{\forall }$, $\mathsf{co}\mathsf{RP}=\mathrm{\forall }/\mathsf{Я}$, $\mathsf{MA}=\mathrm{\exists }\mathsf{Я}/\mathrm{\forall }\mathsf{Я}$, and $\mathsf{AM}=\mathsf{Я}\mathrm{\exists }/\mathsf{Я}\mathrm{\forall }$. In general, to take the “$\mathsf{co}$” of a class, you simply swap both sides of the slash.

The tricks in our hands

Let’s recall the tools at our disposal: three easy ones, and the two we just proved.

Weaken: $\mathrm{\forall }\Rightarrow \mathsf{Я}\Rightarrow \mathrm{\exists }$

This one is purely logical: we can always turn a $\mathrm{\forall }$ into a $\mathsf{Я}$, and a $\mathsf{Я}$ into $\mathrm{\exists }$, because this only weakens the guarantee. In words: “if all, then most, and if most, then some”. As an example, this shows that $\mathsf{RP}=\mathsf{Я}/\mathrm{\forall }\subseteq \mathrm{\exists }/\mathrm{\forall }=\mathsf{NP}$.

Specialize: $\mathrm{\exists }\mathrm{\forall }\Rightarrow \mathrm{\forall }\mathrm{\exists }$

Another purely logical one: we can swap $\mathrm{\exists }\mathrm{\forall }$ into $\mathrm{\forall }\mathrm{\exists }$, because all this does is to allow the $\mathrm{\exists }$ quantifier to specify more. In words: “if a song is liked by everyone, then everyone has a song that they like”.

In fact, this principle also extends well to $\mathsf{Я}$,² if you think of $\mathsf{Я}$ as sort of “halfway in between $\mathrm{\exists }$ and $\mathrm{\forall }$”:

• you can swap $\mathrm{\exists }\mathsf{Я}\to \mathsf{Я}\mathrm{\exists }$, because “if a song is liked by most people, then most people have a song that they like”;
• you can swap $\mathsf{Я}\mathrm{\forall }\to \mathrm{\forall }\mathsf{Я}$, because “if most people like all songs, then all songs are liked by most people”.

Combine: $\mathrm{\forall }\mathrm{\forall }=\mathrm{\forall }$

If we have the same quantifier twice, then we can reduce it to a single quantifier. For example, suppose we were to define a dumb class $\mathrm{\exists }\mathrm{\exists }/\mathrm{\forall }\mathrm{\forall }$, i.e.

• if $x\in L$, then $\mathrm{\exists }y,\mathrm{\exists }z:V(x,y,z)=1$;
• if $x\notin L$, then $\mathrm{\forall }y,\mathrm{\forall }z:V(x,y,z)=0$.

Then we could just combine strings $y$ and $z$ together:

• if $x\in L$, then $\mathrm{\exists }(y,z):V(x,y,z)=1$;
• if $x\notin L$, then $\mathrm{\forall }(y,z):V(x,y,z)=0$.

And this is now functionally equivalent to $\mathrm{\exists }/\mathrm{\forall }=\mathsf{NP}$.

Union bound: $\mathrm{\forall }\mathsf{Я}=\mathsf{Я}\mathrm{\forall }$

The key of the proof of $\mathsf{BPP}\subseteq \mathsf{P}/\mathrm{poly}$ was to boost the success probability so much that we can go from “for all inputs $x$, most random strings $r$ give the correct answer” to “most random strings $r$ give the correct answer for all inputs $x$” by a union bound. In general, we can always³ flip $\mathrm{\forall }\mathsf{Я}$ into $\mathsf{Я}\mathrm{\forall }$ (even though this is the “wrong” direction in terms of direct implication).

In words: “if there’s more songs than people, and everyone likes all but a handful of songs, then most songs are liked by literally everyone”.

Squint: $\mathsf{Я}/\mathsf{Я}\subseteq \mathsf{Я}\mathrm{\forall }/\mathrm{\forall }\mathsf{Я}$

In the proof that $\mathsf{BPP}\subseteq {\mathrm{\Sigma }}_2\mathsf{P}$, we saw that if we have a set $S$ of random strings covering almost all of ${\{0,1\}}^s$, then the union of random offset copies $(S\oplus d^{(1)})\cup \cdots \cup (S\oplus d^{(s)})$ covers all of ${\{0,1\}}^s$ with high probability, while if $S$ contains almost none of ${\{0,1\}}^s$, then no matter what offsets you choose, the offset copies will still cover only a tiny fraction of ${\{0,1\}}^s$. That is, after boosting the success probability,

• $\mathsf{Я}r:V(x,r)=1$ implies $\mathsf{Я}{d}^{(1)},\dots ,d^{(s)},\mathrm{\forall }r:V(x,r\oplus d^{(1)})\vee \cdots \vee V(x,r\oplus d^{(s)})=1$;
• $\mathsf{Я}r:V(x,r)=0$ implies $\mathrm{\forall }{d}^{(1)},\dots ,d^{(s)},\mathsf{Я}r:V(x,r\oplus d^{(1)})\vee \cdots \vee V(x,r\oplus d^{(s)})=0$.

So⁴ we can transform $\mathsf{Я}/\mathsf{Я}$ into $\mathsf{Я}\mathrm{\forall }/\mathrm{\forall }\mathsf{Я}$.

In words: “an almost full jar will typically look full if you squint, but an almost empty jar will always look mostly empty no matter how you squint”.

Also, by taking the “$\mathsf{co}$” of both sides, we also get $\mathsf{Я}/\mathsf{Я}\to \mathrm{\forall }\mathsf{Я}/\mathsf{Я}\mathrm{\forall }$. This corresponds to taking the intersection of the offset copies $(S\oplus d^{(1)})\cap \cdots \cap (S\oplus d^{(s)})$ instead of the union (and therefore the AND instead of the OR). This ensures that when $S$ covers almost all of ${\{0,1\}}^s$, the intersection is still big, while if $S$ contains almost none of ${\{0,1\}}^s$, the intersection will be completely empty with high probability.

A slurry of corollaries

We’ve done all the hard thinking work, now we get to play around with quantifiers!

A alternative characterization of $\mathsf{BPP}$

The proof that $\mathsf{BPP}\subseteq {\mathrm{\Sigma }}_2\mathsf{P}$ that we saw before really went through an intermediate class $\mathsf{Я}\mathrm{\forall }/\mathrm{\forall }\mathsf{Я}$:

$$\mathsf{BPP}=\mathsf{Я}/\mathsf{Я}\stackrel{\text{squint}}{\subseteq }\mathsf{Я}\mathrm{\forall }/\mathrm{\forall }\mathsf{Я}\stackrel{\text{weaken}}{\subseteq }\mathrm{\exists }\mathrm{\forall }/\mathrm{\forall }\mathrm{\exists }={\mathrm{\Sigma }}^2\mathsf{P}.$$

As it turns out, $\mathsf{Я}\mathrm{\forall }/\mathrm{\forall }\mathsf{Я}$ is equal to $\mathsf{BPP}$, since

$$\mathsf{Я}\mathrm{\forall }/\mathrm{\forall }\mathsf{Я}\stackrel{\text{weaken}}{\subseteq }\mathsf{Я}\mathsf{Я}/\mathsf{Я}\mathsf{Я}\stackrel{\text{combine}}{=}\mathsf{Я}/\mathsf{Я}=\mathsf{BPP}.$$

One-sided error for $\mathsf{MA}$ and $\mathsf{AM}$

Both $\mathsf{MA}$ and $\mathsf{AM}$ correspond to two-round proof protocols between Arthur, a weak but honest mortal with the power of $\mathsf{BPP}$, and Merlin, a powerful but untrustworthy wizard with unbounded computation power (Merlin kind of plays the role of $\mathsf{NP}$ here).

The two classes vary only in who goes first:

• In $\mathsf{MA}:=\mathrm{\exists }\mathsf{Я}/\mathrm{\forall }\mathsf{Я}$, Merlin first sends a purported “proof” that $x\in L$, then Arthur uses randomness to “verify” the proof.
• In $\mathsf{AM}:=\mathsf{Я}\mathrm{\exists }/\mathsf{Я}\mathrm{\forall }$, Arthur first uses randomness to create an $\mathsf{NP}$-type “challenge” for Merlin (e.g. a SAT instance), then Merlin tries to find a “solution” to the challenge.

The same squinting trick that gives “absolute guarantees” for $\mathsf{BPP}$ at the cost of an extra quantifier can also give absolute guarantees for $\mathsf{MA}$ and $\mathsf{AM}$, but this time for free: Merlin’s $\mathrm{\exists }/\mathrm{\forall }$ quantifier can absorb one of the two quantifiers that appear.

Formally,

$$\mathsf{MA}=\mathrm{\exists }\mathsf{Я}/\mathrm{\forall }\mathsf{Я}\stackrel{\text{squint}}{\subseteq }\mathrm{\exists }(\mathsf{Я}\mathrm{\forall })/\mathrm{\forall }(\mathrm{\forall }\mathsf{Я})\stackrel{\text{weaken}}{\subseteq }\mathrm{\exists }\mathrm{\exists }\mathrm{\forall }/\mathrm{\forall }\mathrm{\forall }\mathsf{Я}\stackrel{\text{combine}}{=}\mathrm{\exists }\mathrm{\forall }/\mathrm{\forall }\mathsf{Я}.$$

In effect, we asked Merlin to attach to his proof the offsets $d^{(1)},\dots ,d^{(s)}$ that make sure that Arthur always accepts when $x\in L$. This means that there are no “false negatives” anymore. Also, since $\mathrm{\exists }\mathrm{\forall }/\mathrm{\forall }\mathsf{Я}\subseteq \mathrm{\exists }\mathrm{\forall }/\mathrm{\forall }\mathrm{\exists }$ by weakining, this shows that $\mathsf{MA}\subseteq {\mathrm{\Sigma }}_2\mathsf{P}$.

Similarly, for $\mathsf{AM}$,

$$\mathsf{AM}=\mathsf{Я}\mathrm{\exists }/\mathsf{Я}\mathrm{\forall }\stackrel{\text{squint}}{\subseteq }(\mathrm{\forall }\mathsf{Я})\mathrm{\exists }/(\mathsf{Я}\mathrm{\forall })\mathrm{\forall }\stackrel{\text{weaken}}{\subseteq }\mathrm{\forall }\mathrm{\exists }\mathrm{\exists }/\mathsf{Я}\mathrm{\forall }\mathrm{\forall }\stackrel{\text{combine}}{=}\mathrm{\forall }\mathrm{\exists }/\mathsf{Я}\mathrm{\forall }.$$

This time, we used the “$\mathsf{co}$” version of squinting, and Arthur is only drawing the offsets, while Merlin tries to find a random string such that the verifier accepts on all the offsets. When $x\in L$, Merlin is always able to succeed, so there are no “false negatives”. Also, since $\mathrm{\forall }\mathrm{\exists }/\mathsf{Я}\mathrm{\forall }\subseteq \mathrm{\forall }\mathrm{\exists }/\mathrm{\exists }\mathrm{\forall }$ by weakning, this implies $\mathsf{AM}\subseteq {\mathrm{\Pi }}_2\mathsf{P}$.

$\mathsf{MA}\subseteq \mathsf{AM}$

On a surface level, $\mathsf{MA}$ and $\mathsf{AM}$ seem incomparable: they’re the same class with the order of quantifiers flipped, just like ${\mathrm{\Sigma }}_2\mathsf{P}$ and ${\mathrm{\Pi }}_2\mathsf{P}$. But it turns out that $\mathsf{MA}\subseteq \mathsf{AM}$: it’s always better for Arthur to go first.

• For $x\in L$, this is true because $\mathrm{\exists }\mathsf{Я}$ logically implies $\mathsf{Я}\mathrm{\exists }$: the only thing that changes between $\mathsf{MA}$ and $\mathsf{AM}$ is that Merlin now gets to see Arthur’s coin flips before sending his message, so that can only help him make Arthur accept.
• For $x\notin L$, on the other hand (and for the same reasons), $\mathrm{\forall }\mathsf{Я}$ does not directly imply $\mathsf{Я}\mathrm{\forall }$: even if no message of Merlin can fool Arthur on average when Merlin goes first, once the order is flipped, Merlin might be able to do better by adaptively choosing which message to send based on Arthur’s message. But if the probability Arthur is fooled is small compared to the number of possible messages for Merlin, then most of the time Arthur cannot be fooled by any message.

In math, this gives

$$\mathsf{MA}=\mathrm{\exists }\mathsf{Я}/\mathrm{\forall }\mathsf{Я}\stackrel{\text{specialize}}{\subseteq }\mathsf{Я}\mathrm{\exists }/\mathrm{\forall }\mathsf{Я}\stackrel{\text{union bound}}{=}\mathsf{Я}\mathrm{\exists }/\mathsf{Я}\mathrm{\forall }=\mathsf{AM}.$$

Overall, we can summarize what we know about these classes in this diagram (classes that are generally believed to be equal are shaded together):

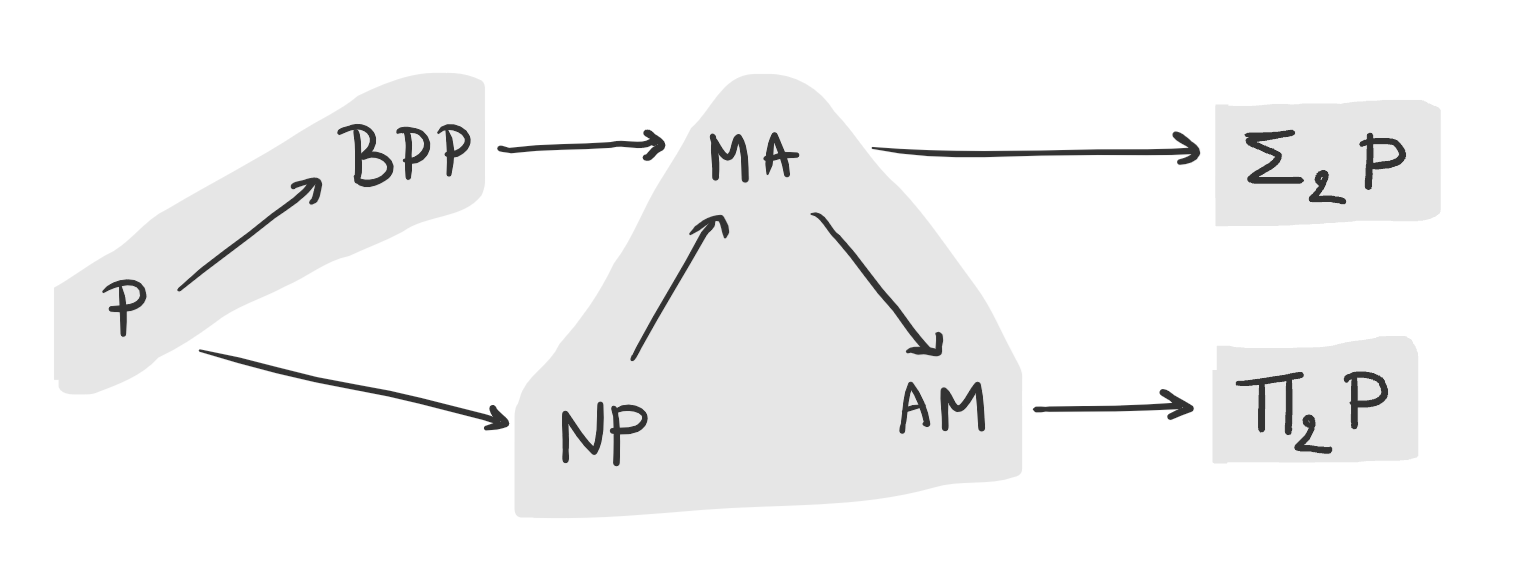
Constant-round protocols are all in $\mathsf{AM}$

One might think that by adding more rounds of interaction between Arthur and Merlin, we can keep extending the class of languages. But this is not the case! The reason is the intuition that we got from the previous section: it’s always better for Arthur to go before Merlin, so we can transform the protocol so that Arthur sends all of his messages first, then Merlin sends all of his messages.

For example, consider the class $\mathsf{AMA}$ where Arthur goes first and last. Informally, we know that $\mathsf{MA}\subseteq \mathsf{AM}$, so it’s tempting to write $\mathsf{AMA}\subseteq \mathsf{AAM}=\mathsf{AM}$. This is not quite how math works but it’s fundamentally the right idea. More formally, we can write $\mathsf{AMA}$ as $\mathsf{Я}\mathrm{\exists }\mathsf{Я}/\mathsf{Я}\mathrm{\forall }\mathsf{Я}$,⁵ so we can pull the same trick where we flip $\mathrm{\exists }\mathsf{Я}/\mathrm{\forall }\mathsf{Я}$ into $\mathsf{Я}\mathrm{\exists }/\mathsf{Я}\mathrm{\forall }$, then combine quantifiers.

$$\mathsf{AMA}=\mathsf{Я}\mathrm{\exists }\mathsf{Я}/\mathsf{Я}\mathrm{\forall }\mathsf{Я}\stackrel{\text{specialize}}{\subseteq }\mathsf{Я}\mathsf{Я}\mathrm{\exists }/\mathsf{Я}\mathrm{\forall }\mathsf{Я}\stackrel{\text{union bound}}{=}\mathsf{Я}\mathsf{Я}\mathrm{\exists }/\mathsf{Я}\mathsf{Я}\mathrm{\forall }\stackrel{\text{combine}}{=}\mathsf{Я}\mathrm{\exists }/\mathsf{Я}\mathrm{\forall }=\mathsf{AM}.$$

What if $\mathsf{NP}\subseteq \mathsf{BPP}$?

In complexity we often think of $\mathsf{P}$ as the definition of “efficient computation”. But what would happen if we used $\mathsf{BPP}$ instead?

One important result is to show that if $\mathsf{NP}$ was “easy” (i.e. $\mathsf{P}=\mathsf{NP}$), then dramatic things would happen (i.e. the polynomial hierarchy would collapse). What would happen if $\mathsf{NP}\subseteq \mathsf{BPP}$?

If we had an $\mathsf{NP}$ oracle within $\mathsf{BPP}$, then in particular, we could use it to solve ${\mathrm{\Sigma }}_2\mathsf{P}$ within $\mathsf{MA}$: use Merlin for the first quantifier, then let Arthur use the $\mathsf{NP}$ oracle to handle the second quantifier:

$${\mathrm{\Sigma }}_2\mathsf{P}=\mathrm{\exists }\mathrm{\forall }/\mathrm{\forall }\mathrm{\exists }\stackrel{\mathsf{NP}\subseteq \mathsf{BPP}}{\subseteq }\mathrm{\exists }\mathsf{Я}/\mathrm{\forall }\mathsf{Я}=\mathsf{MA}.$$

But we know $\mathsf{MA}\subseteq \mathsf{AM}\subseteq {\mathrm{\Pi }}_2\mathsf{P}$. So we would have ${\mathrm{\Sigma }}_2\mathsf{P}\subseteq {\mathrm{\Pi }}_2\mathsf{P}$ and the polynomial hierarchy would collapse to the second level.

Appendix: I lied a bit

This appendix is boring, please don’t read it.

I claimed earlier that we can always replace $\mathrm{\forall }\mathsf{Я}$ by $\mathsf{Я}\mathrm{\forall }$, and $\mathsf{Я}/\mathsf{Я}$ by $\mathsf{Я}\mathrm{\forall }/\mathrm{\forall }\mathsf{Я}$. Well, it’s a bit more complicated. The thing is, these tricks required some change to the computation that follows:

• For the “union bound” in $\mathrm{\forall }\mathsf{Я}\to \mathsf{Я}\mathrm{\forall }$ to work, we need to boost the probability of success. This involves repeating the computation several times in parallel and taking the majority of the answers.
• For the “squinting” trick in $\mathsf{Я}/\mathsf{Я}\to \mathsf{Я}\mathrm{\forall }/\mathrm{\forall }\mathsf{Я}$ we need to first boost the probability of succes then run this boosted computation at several offsets $d^{(1)},\dots ,d^{(s)}$ and take the OR.

This means that we should be able to take majorities or ORs in the underlying computation model. For $\mathsf{BPP}$, this was no problem: once $x$ and $r$ are chosen, the remaining computation $V(x,r)$ is deterministic polynomial time, so repeating $\mathrm{poly}(n)$ times and computing the majority is no big deal. On the other hand, imagine we’re looking at $\mathsf{AM}=\mathsf{Я}\mathrm{\exists }/\mathsf{Я}\mathrm{\forall }$. Then the computation that follows the “for most” quantifier is an $\mathsf{NP}$-type computation. Can we compute the majority of some $\mathsf{NP}$ computations within $\mathsf{NP}$ itself? Given that we cannot even easily negate the result of an $\mathsf{NP}$ computation (unless $\mathsf{NP}=\mathsf{co}\mathsf{NP}$), this seems worrying.

However, it does turn out to be okay, and ultimately this comes down to the fact that you can push monotone operations like $\wedge$ and $\vee$ inside quantifiers $\mathrm{\exists }$ and $\mathrm{\forall }$:⁶ for example <div>[(\exists y_1 : P(y_1)) \and (\exists y_2 : P(y_2)) \Leftrightarrow \exists y_1, y_2: P(y_1) \and P(y_2).]</div> Concretely, for boosting probabilities, we get

• if $x\in L$, then $\mathsf{Я}{r}_1,\dots ,r_k:{\mathrm{Maj}}_i(\mathbb{1}[\mathrm{\exists }y:V(x,r_i,y))=1])=1$;
• if $x\notin L$, then $\mathsf{Я}{r}_1,\dots ,r_k:{\mathrm{Maj}}_i(\mathbb{1}[\mathrm{\forall }y:V(x,r_i,y)=0])=1$.

Which is equivalent to

• if $x\in L$, then $\mathsf{Я}{r}_1,\dots ,r_k,\mathrm{\exists }{y}_1,\dots ,y_k:{\mathrm{Maj}}_i(V(x,r_i,y))=1$;
• if $x\notin L$, then $\mathsf{Я}{r}_1,\dots ,r_k,\mathrm{\forall }{y}_1,\dots ,y_k:{\mathrm{Maj}}_i(V(x,r_i,y))=0$.

1. All strings are understood to have length polynomial in $n:=|x|$. ↩

2. In fact, as already mentioned in a footnote in Buying randomness with quantifiers, you can always move $\mathrm{\exists }$ to the inside (because you can just choose not to specialize) and $\mathrm{\forall }$ to the outside (because if it always works, it cannot meaningfully specialize): whatever (monotone) quantifier $Q$ you might come up with, $\mathrm{\exists }Q\to Q\mathrm{\exists }$ and $Q\mathrm{\forall }\to \mathrm{\forall }Q$. But we’re getting carried away! ↩

3. Actually, this is only the case if the underlying computation model allows us to boost the probability of success, see more details in the appendix. ↩

4. Actually, this is only the case if the underlying computation model allows us to boost the probability of success and compute ORs of polynomially many runs, see more details in the appendix. ↩

5. Actually even the claim that $\mathsf{AMA}=\mathsf{Я}\mathrm{\exists }\mathsf{Я}/\mathsf{Я}\mathrm{\forall }\mathsf{Я}$ is not obvious. The protocol-based definition only promises an overall probability of success, not that Arthur “succeeds with high probability at every round”. You can (very carefully) prove it by parallel repetition, though. ↩

6. in this note, we won’t need to boost the probability for a computation that itself includes $\mathsf{Я}$. Ironically, for $\mathsf{Я}$, it’s less easy, but you can indeed do it… as long as the probability of that $\mathsf{Я}$ is high enough. So as far as I can tell, if you want to boost the probability of some $\mathsf{Я}$, you need to first boost the $\mathsf{Я}$’s right of it. ↩